Предмет: Алгебра,
автор: polinaholi49
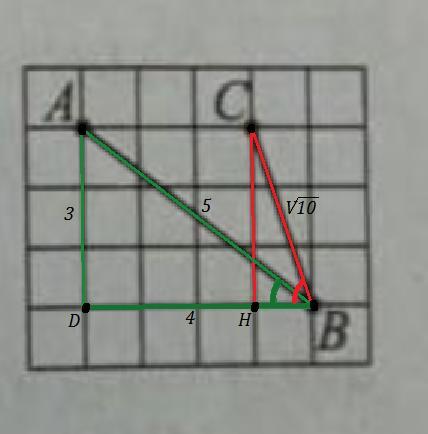
На координатной плоскости отмечены точки А, B ,C ,см.рисунок. Найдите синус угла АВС. В ответе укажите значение синуса умноженное на корень из 10
p.s : в ответе должно получиться 1,8 , но как?
Приложения:

Ответы
Автор ответа:
2
Ответ:1, 8
Объяснение:
Приложения:

irinan2014:
Можно решать по теореме косинусов.
Автор ответа:
1
Ответ:
Проведём два перпендикуляра АD⊥ BD и CH ⊥ BD .
∠CBD=α , ∠ABD=β
∠ABC=∠CBD-∠ABD=α-β
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: mashashelakina
Предмет: Русский язык,
автор: de2002
Предмет: Русский язык,
автор: svetlana00059
Предмет: Другие предметы,
автор: paerelid
Предмет: Русский язык,
автор: ya1katyabro