Пожалуйста решите, срочно

Ответы
Ответ:
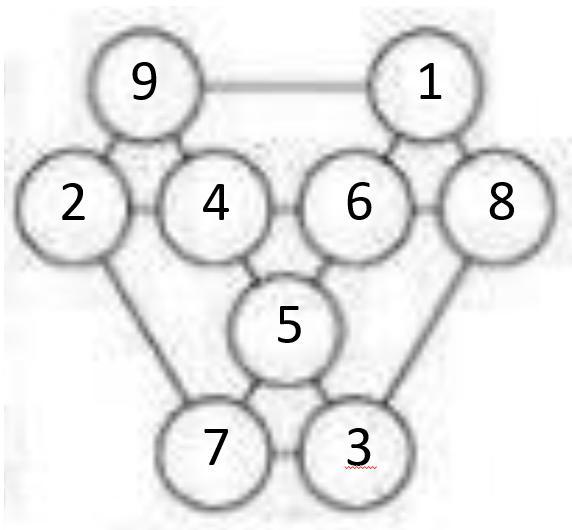
одно из решений представлено во втором вложении
Пошаговое объяснение:
Анализируя схему и числа, которыми ее надо заполнить, можно обратить внимание на следующее:
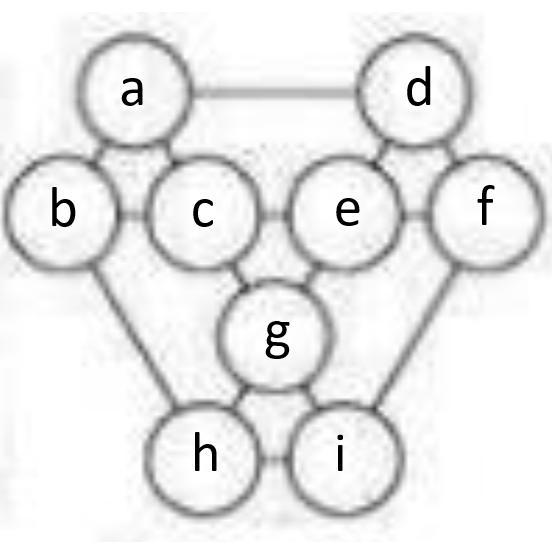
1) три малых треугольника (у меня в первом вложении они по буквам в кружках обозначены abc, def и ghi), во-первых, не содержат общих вершин, а во-вторых, охватывают все 9 кружков. Сумма всех используемых чисел равна = 45, и суммы чисел для каждого треугольника одни и те же, стало быть они равны 45:3 = 15
2) существуют только две суммы трех различных натуральных чисел, одно из которых 9, равные 15, а именно: 1+5+9 и 2+4+9; а также две суммы с аналогичными свойствами, но в которых одно из чисел — 1, а именно: 1+5+9 и 1+6+8. Поскольку "внутренние" кружки c, e и g принимают участие в образовании трех треугольников каждый и в любых двух различных треугольниках тройки чисел, стоящих в их вершинах, полностью не совпадают (ведь числа не повторяются), числа 9 и 1 могут стоять только во "внешних" кружках a, b, d, f, h, i.
Внесем число 9, например, в кружок a. Допустим, мы хотим в одну из вершин d и g вписать 1, а в другую — 5. Исходя из выводов, сделанных в пункте 2), имеет смысл только вариант d=1, g=5. А вот шаг, на котором мы будем заполнять кружки b и c числами 2 и 4, предоставляет право выбора: в обоих случаях оставшиеся вершины заполняются однозначно и получается требуемый результат. Решение, где b=2, приведено во вложении. Впрочем, оно далеко не единственное. Например, в начале мы могли числа 1 и 5 внести в кружки b и c соответственно и тоже пришли бы к какому-нибудь корректному заполнению.