Question

Задача с конусом!! Вычислить наибольший объём конуса, если длина образующей равна 43,8 см:

V = [пропуск] * √[пропуск] π см³

Answer 1

Ответ:

V = 6224,272 * √3 π см³

Объяснение:

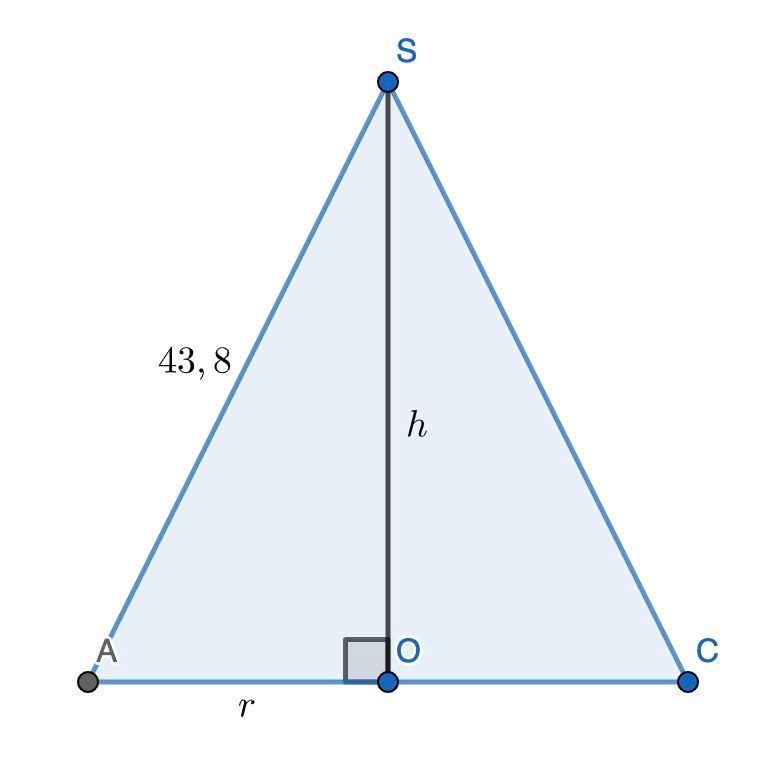
Рассмотрим осевое сечение конуса (см. рис.). SO — высота конуса (h), AO — радиус (r), AS — образующая конуса (43,8 см). Тогда по теореме Пифагора r² + h² = 43,8².

Объём конуса вычисляется по формуле $V=\dfrac{1}{3}\pi r^2h$. Из предыдущего уравнения r² = 43,8² - h². Подставим это в уравнение объёма:

$V=\dfrac{1}{3}\pi (43{,}8^2-h^2)h=\dfrac{43{,}8^2\pi}{3}h-\dfrac{\pi}{3}h^3$

Найдём максимальное значение с помощью производной:

$V'(h)=\dfrac{43{,}8^2\pi}{3}-\pi h^2\\V'(h)=0\Leftrightarrow \dfrac{43{,}8^2\pi}{3}=\pi h^2\Leftrightarrow h=\pm\dfrac{43{,}8}{\sqrt{3}}$

Будем рассматривать только положительные значения h, так как отрицательной высота быть не может. При $0<h<\dfrac{43{,}8}{\sqrt{3}}\ V'(h)>0$, при $h>\dfrac{43{,}8}{\sqrt{3}}\ V'(h)<0$. Значит, $h=\dfrac{43{,}8}{\sqrt{3}}$ — точка максимума. При данном значении h объём конуса максимален.

$V_{\max}=\dfrac{1}{3}\pi\left(43{,}8^2-\dfrac{43{,}8^2}{3}\right)\cdot\dfrac{43{,}8}{\sqrt{3}}=\dfrac{1}{3}\pi \cdot\dfrac{2}{3}\cdot 43{,}8\cdot 43{,}8\cdot\dfrac{43{,}8}{3}\sqrt{3}=\\=14{,}6\cdot 2\cdot 14{,}6\cdot 14{,}6\sqrt{3}\pi=6224{,}272\sqrt{3}\pi$