Предмет: Алгебра,
автор: Аноним
напишите решение уравнения
Приложения:
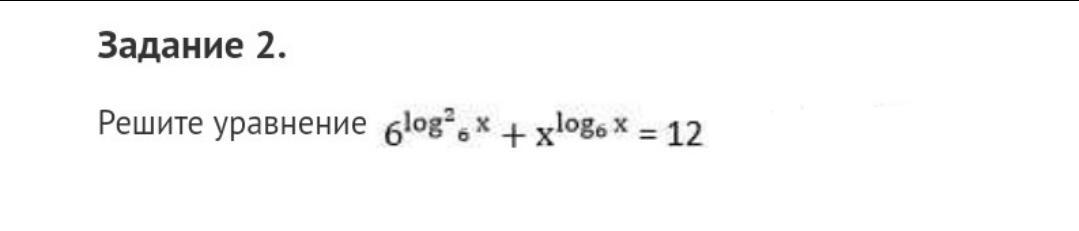
Ответы
Автор ответа:
0
Ответ:
Объяснение:
ОДЗ: x > 0
Оба корня положительны, следовательно, они удовлетворяют ОДЗ.
Похожие вопросы
Предмет: Русский язык,
автор: Arinazlat
Предмет: Русский язык,
автор: ппп113
Предмет: Русский язык,
автор: pushkinae
Предмет: Русский язык,
автор: slavaselivanov
Предмет: Химия,
автор: muxit1235698776