Предмет: Алгебра,
автор: ChelovekGeniy
Здравствуйте, помогите, пожалуйста, с решением уравнения и объясните его решение, пожалуйста
Приложения:
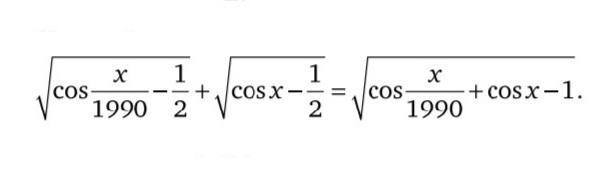
LFP:
если выражение под первым корнем обозначить а=cos(x/1990)-(1/2); выражение под вторым корнем обозначить b=cos(x)-(1/2), то получится уравнение √a + √b = √(a+b)... это возможно только при а=0 или и=0
...или b=0
Ответы
Автор ответа:
1
Ответ:
Объяснение:
В комментарии всё правильно написано. Делаем замену:
Получаем:
√a + √b = √(a+b)
Это возможно только в трех случаях:
1)
x/1990 = +-П/3 + 2Пk
x1 = +-1990П/3 + 3980Пk, k ∈ Z
2)
cos x = 1/2
x2 = +-П/3 + 2Пk, k ∈ Z
3)
То есть 1) и 2) одновременно. Но этот случай решений не имеет.
Автор ответа:
3
Ответ:
Объяснение:
Дано уравнение
ОДЗ:
Преобразуем уравнение и вводим обозначения:
Тогда получим уравнение
Учитывая ОДЗ возведём оба части уравнения в квадрат и упростим:
Далее, сделаем обратную подстановку и решаем уравнение:
Похожие вопросы
Предмет: Русский язык,
автор: marya4
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: лиза464
Предмет: Биология,
автор: Fawnal