Question

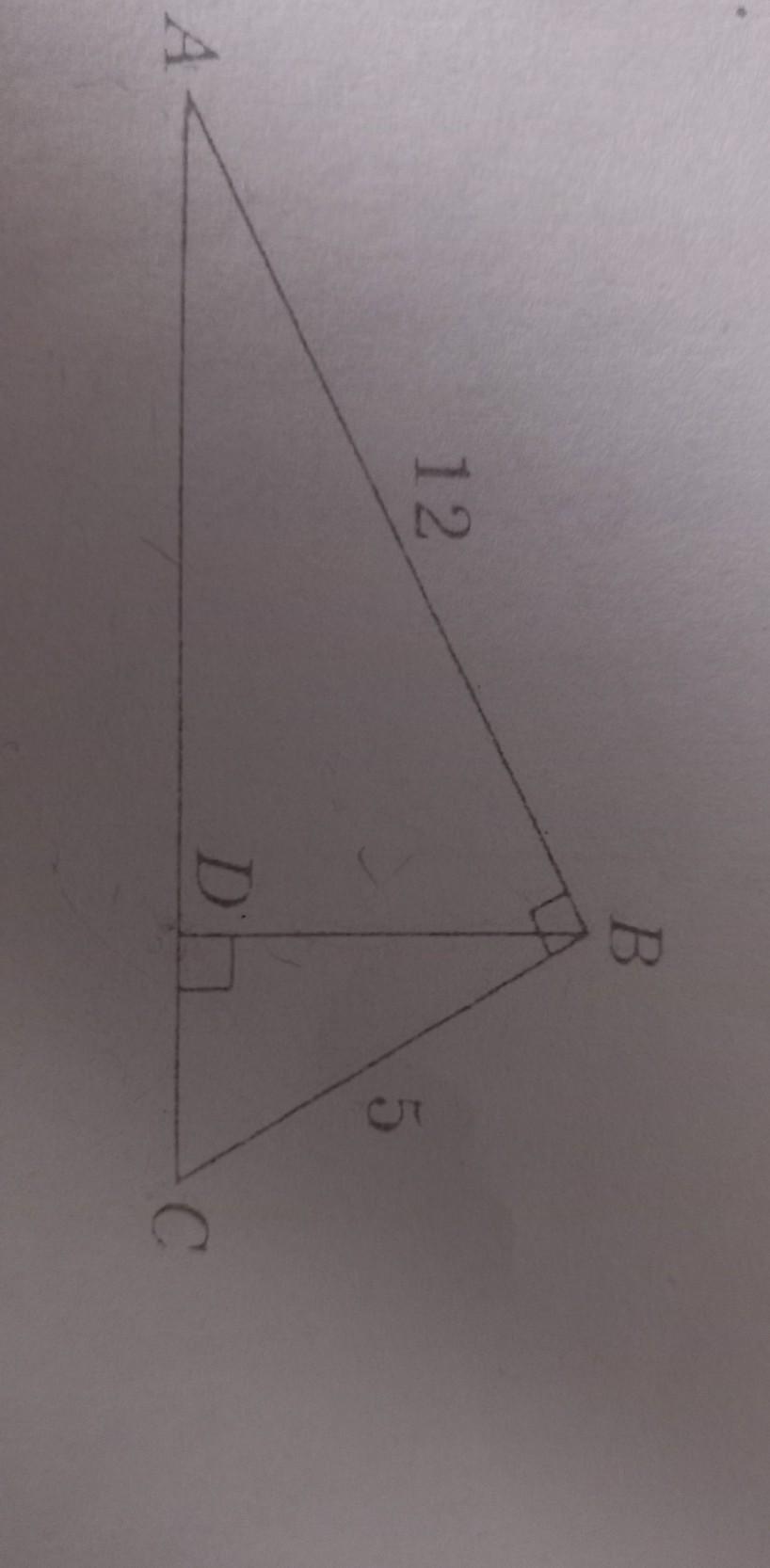
Дано угол ABC =90°; BDпараллелен AC; AB=12; BC =5. Найти BD​

Answer 1

Ответ:

4цел8/13

Объяснение:

Теорема Пифагора

АС=√(АВ²+ВС²)=√(5²+12²)=√(25+144)=

=√169=13

BD=AB*BC/AC=5*12/13=60/13=4цел8/13

Answer 2

1) Найдём гипотенузу АС по теореме Пифагора:

$AC = \sqrt{12^2+5^2} = \sqrt{144+25} = \sqrt{169} = 13$

2) Находим угол ВАС через соотношение прилегающего катета и гипотенузы, иначе говоря cos:

$\frac{12}{13} = 0,923$

arccos 0.923 = 22° (приблизительно)

Возьмём на заметку, что: следуя из приблизительности, конечный результат тоже будет приблизительный

Отсюда, угол АВD = 180 - (90 + 22) = 68°

Через cos мы можем вывести следующее:

$\frac{BD}{12} = \frac{374}{1000}\\BD = \frac{374*12}{1000} = 4.488\\4.488 = 4\frac{61}{125}$

Ответ: $4\frac{61}{125}$