Предмет: Математика,
автор: ruslangal26
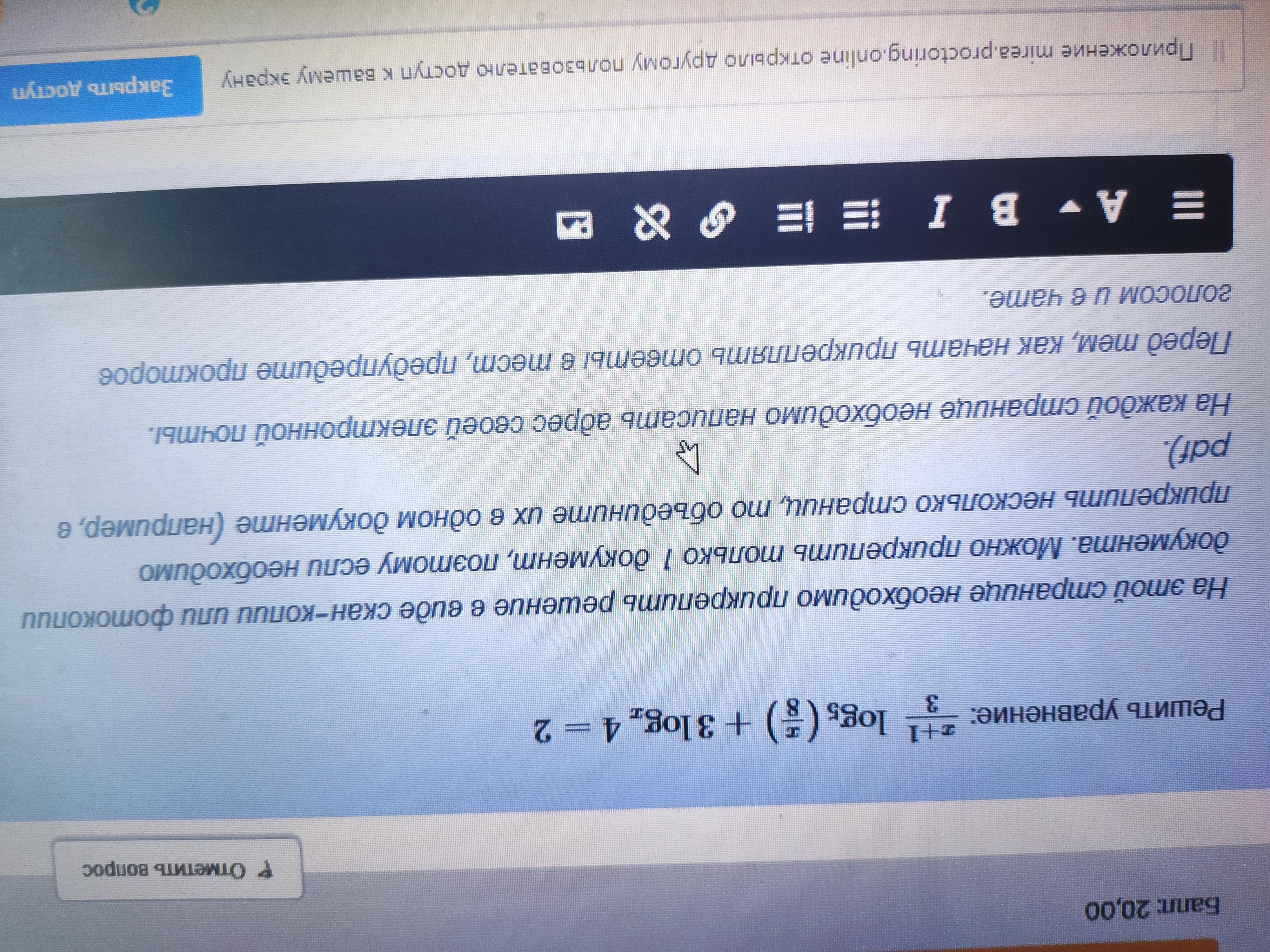
Решить уравнение с логарифмами. Очень нужна помощь
Приложения:
tamarabernukho:
https://znanija.com/task/45122350
Ответы
Автор ответа:
0
Ответ:
5; 8
Пошаговое объяснение:
ОДЗ: x > 0, x ≠ 1
Учитывая ОДЗ, домножим уравнение на , а также обозначим
для удобства:
ИЛИ
На промежутке x > 1 слева представлено произведение двух положительных монотонно возрастающих функций. Значит, на данном промежутке левая часть — монотонно возрастающая функция, принимающая каждое значение ровно один раз. Значит, при x > 1 уравнение имеет не более одного корня. Действительно, при x = 5 равенство выполняется.
На промежутке 0 < x < 1 . На данном промежутке решений быть не может. Остальные промежутки числовой оси не удовлетворяют ОДЗ.
Таким образом, уравнение имеет два решения: 5 и 8.
Похожие вопросы
Предмет: Окружающий мир,
автор: космик66
Предмет: Английский язык,
автор: crossfirevito
Предмет: Окружающий мир,
автор: 55555178
Предмет: Химия,
автор: Никитов123322
Предмет: Окружающий мир,
автор: Limonchik1234