Предмет: Алгебра,
автор: yugolovin
Решить уравнение 
Ответы
Автор ответа:
4
Ответ:
-√3; √3
Объяснение:
x⁴ + 5x³ + 4x² - 15x - 21 = 0
x⁴ + 5x³ + 7x² - 3x² - 15x - 21 = 0
x²(x² - 3) + 5x(x² - 3) + 7(x² - 3) = 0
(x² + 5x + 7)(x² - 3) = 0
Продолжение на фото
Приложения:
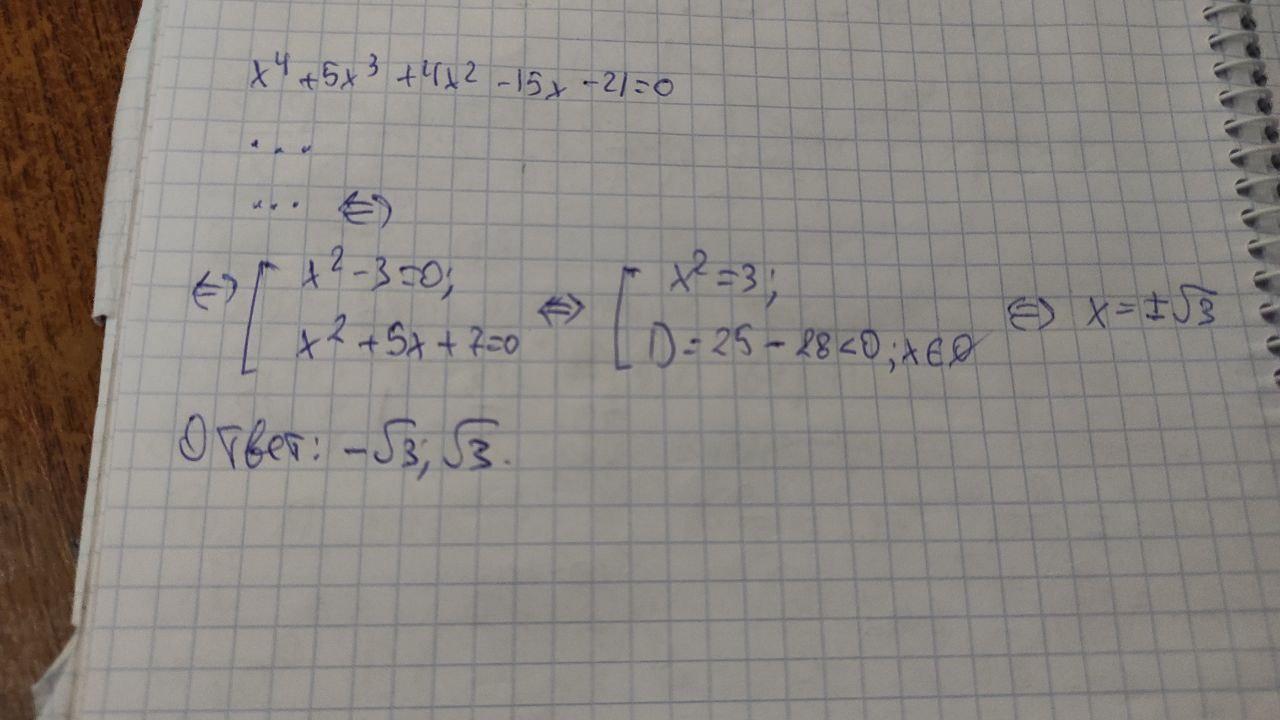
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: httpqpsru7OVCD
Предмет: Английский язык,
автор: slava166
Предмет: Русский язык,
автор: Настя35711
Предмет: Математика,
автор: Luda1111346557