Question

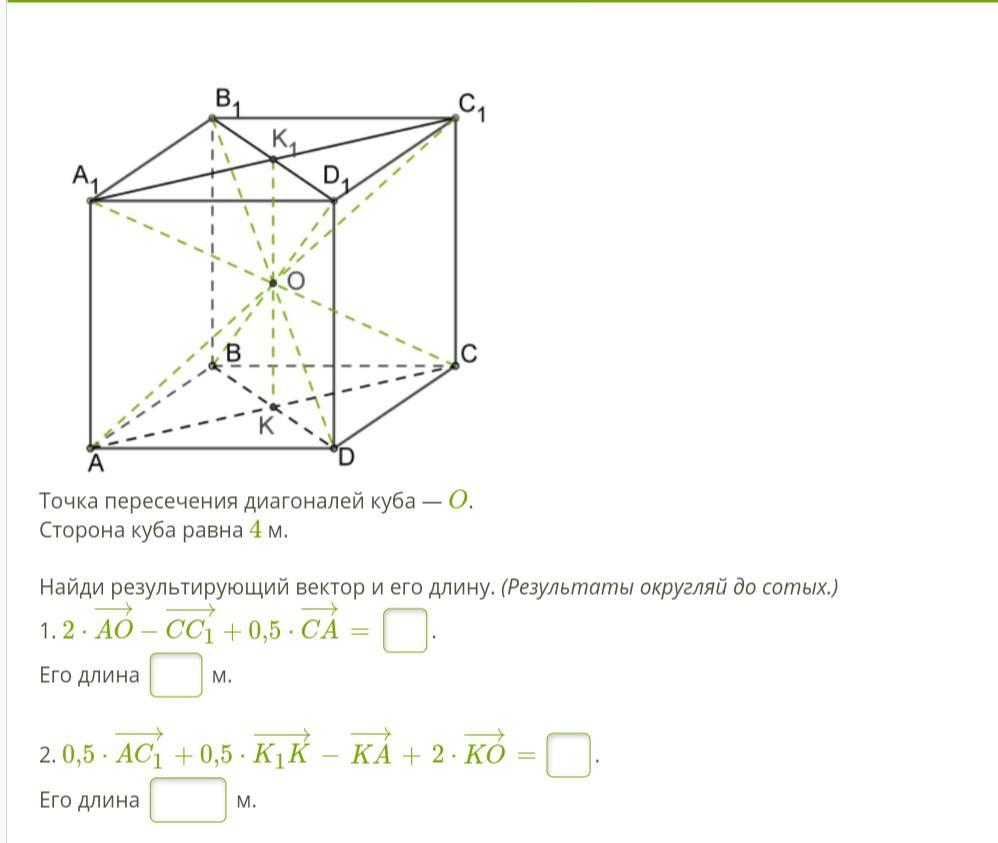
<номер с кубом и векторами>

Answer 1

Решение:

1.

$0.5~\overline {AO}- \overline {CC_1}+0.5~\overline {CA} =\overline {AC_1} - \overline {CC_1}+\overline {KA} = \\ \\ =\overline {AC_1} + \overline {C_1C}+\overline {KA} =\overline {KA} + \overline {AC_1} + \overline {C_1C}=\\ \\=\overline {KC}$

$|\overline {KC}| = 2\sqrt{2} \approx 2.83$

2.

$0.5~\overline {AC_1}+ 0.5~\overline {K_1K }- \overline {KA} + 2~\overline {KO} = \\ \\=\overline {AO} +\overline {OK}+ \overline {AK} + 2~\overline {KO} =\\\\=\overline {AO} + \overline {AK} + 2~\overline {KO} -\overline {KO}=\\ \\=\overline {AO} + \overline {AK} + \overline {KO} =\\ \\=\overline {AC_1} + \overline {AO} = \\ \\=2\overline {AO} =\\ \\=2\overline {AO} =\\ \\=\overline {AC_1}$

$|\overline {AC_1} |= 4\sqrt{3} \approx 6.93$

Answer 2

Ответ:

Объяснение:  

У обох вправах додамо вектори за правилом многокутника .

Задача . 1.  Сума векторів 2AO - CC₁ + 0,5CA = AC₁ + C₁C + CK = AK ;

| AK | = 1/2 | AC | = 1/2 a√2 = 1/2 * 4√2 = 2√2 ( м ) ;  | AK | = 2√2 м .

2.  Сума векторів  0,5AC₁+ 0,5K₁K - KA + 2KO = AO + OK + KC + CC₁ = AC₁ ;

| AC₁ | = √ (AD² + AB² + AA₁² ) = √( 4² + 4² + 4² ) = 4√3 ( м ) ; | AC₁ | = 4√ 3 м .