Решить следующее задание:
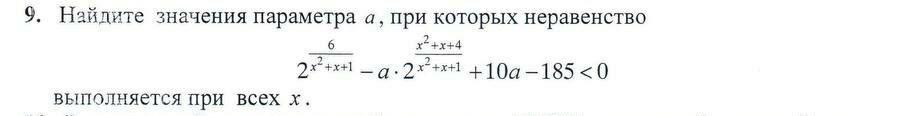
Ответы
Ответ:
(см. объяснение)
Пошаговое объяснение:
Рассмотрим внимательно данное неравенство.
Прежде всего обратим внимание на показатель второй двойки:
Тогда верна запись:
Сделаем замену вида .
Получим неравенство:
Переформулируем условие задачи:
Найти все значения параметра , при каждом их которых записанное выше неравенство содержит промежуток
.
Важным этапом решения будет заметить верхнюю границу для , так как с нижней вроде бы все ясно. Понятно, что для этого надо максимизировать
. В знаменателе дроби видим параболу, наименьшее значение которой достигается в вершине при
. Подставляя это значение в дробь получаем, что она примет значение
. Тогда
.
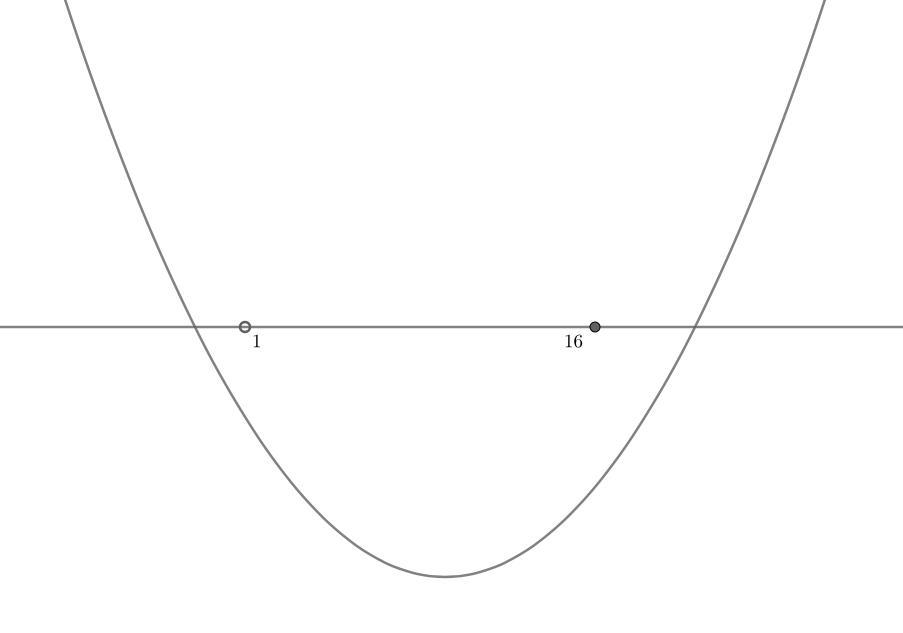
Введем функцию . Это парабола, ветви которой направлены вверх.
Выполним схематичный чертеж:
(см. прикрепленный файл)
Опишем полученное на языке математики:
Тогда решить нужно:
Итого при исходное неравенство выполняется при всех
.
Задание выполнено!