Предмет: Математика,
автор: Frosterion
помогите пожалуйста, в первый раз с такой задачей сталкиваюсь, сколько пробников по ЕГЭ делал не разу такое не попадалось. Мне а то скоро вступительные сдавать, фиг знает как это решать.
"На плоскости хОу с декартовыми координатами задана плоская фигура, координаты точек которой удовлетворяют двойному неравенству:
min {x^2, |x|} меньше или равно y меньше или равно 2".
-найдите наибольшее из целых чисел, не превышающих величину площади фигуры.
-найдите утроенную площадь фигуры.
-найдите радиус окружности, описанной около фигуры.
palilov243659:
"min {x^2, |x|}- это наименьшее из чисел х^2 и |x|, т.е. 0. следовательно, фигура расположена между у=0 и у=2 и ограничена окружностью с центром в точке координатами (х; 1), где х любое действительное число, например=0. радиус окружности=1.
нет , всё не то
наименьшее выбирается из 2 функций , у которой график ниже , та и наименьшая
из двух ординат выбирается наименьшее
мы сравниваем 2 значения x^2 и |x | , то есть ординаты точек , там , где график ниже , та и наименьшая
pailov, при |x|<= 1 . x >=x^2, то есть, при |x|<=1 имеем параболу y = x^2, при |x| > 1 наоборот: x< x^2; y = |x|. И все это ограничено сверху y = 2. То есть фигура это парабола + две прямые
можно взять прямую x = a и начать её двигать , нижняя точка пересечения её с 2 графиками и будет наименьшим значением
Возможно, но я всё равно ЕГЭ сдавать не буду, будут в вступительные испытания в котором по 15 вопросов, прост говорили что по сложности такие же как в ЕГЭ, и попадались даже сложнее
https://image.prntscr.com/image/DWkPMnwLSSqw7LduvUTFRw.jpeg
это пример из ДВИ этого года , я бы не сказал , что он простой
Ответы
Автор ответа:
2
Ответ:
4 ; 13 ; 2
Пошаговое объяснение:
Приложения:
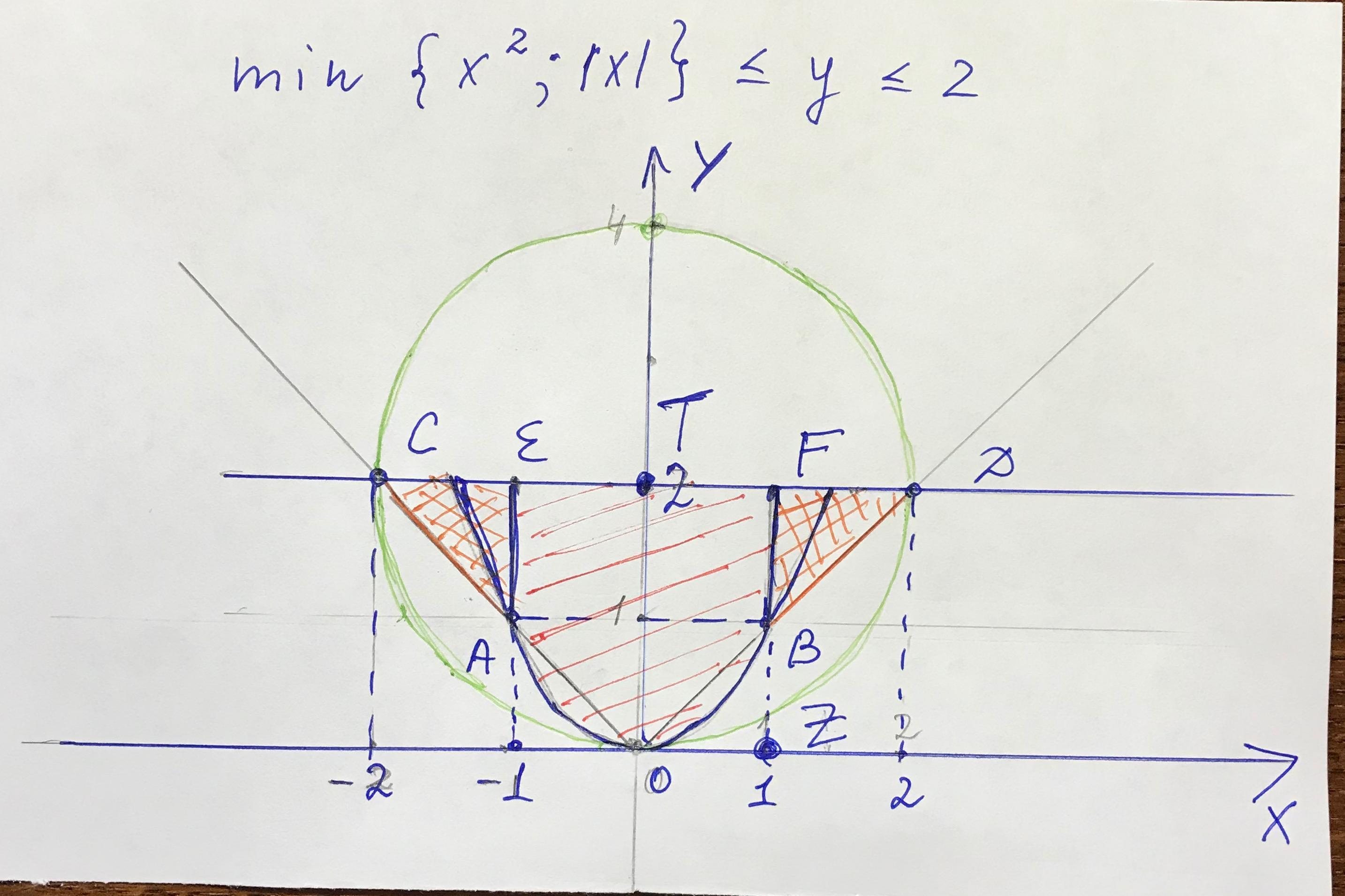


это задание 7 из ЕГЭ , хорошо , что на реальном ЕГЭ таких заданий не бывает , условие школьники могут не понять
Это да. Продвинутое егэ стало
да нет , в этом году очень простое ЕГЭ было , геометрия просто примитивная , это вероятно методисты упражняются
Я бы не разбивал на две половины. Легче сложить площадь части с параболой и трапецию. Площадь части с параболой это прямоугольник - интеграл
Ну хотя тут кому как удобно
меня смущает термин "описанная окружностть": Описанная окру́жность многоугольника — окружность, содержащая все вершины многоугольника. Вершины А и В не входят
Мы уже обсуждали это , условие составлено некорректно
найти наименьший радиус окружности , содержащей данную фигуру - вот так надо было сформулировать последний пункт
Хочу исправить последнее предложение ( неверно , естественно , окружность не может содержать эту фигуру ) , итак : найти наименьший радиус окружности , такой , что круг , ограниченный ею содержит данную фигуру
или проще : найти наименьший радиус круга , содержащего данную фигуру
Похожие вопросы
Предмет: Русский язык,
автор: таня589
Предмет: Русский язык,
автор: TimofaceCritic
Предмет: Русский язык,
автор: Дракончик123
Предмет: Физика,
автор: dianapapyan1