Question

комплексное число z удовлетворяет условию |z-4-3i|=3. Найдите наибольшее значение выражения |z|

помогите пожалуйста

Answer 1

Ответ: 8

Пошаговое объяснение:

Пусть:

$z = x + iy$

$a, b$ - действительные числа.

Тогда:

$|(x-4) + (y-3)i| = 3\\(x-4)^2 + (y-3)^2 = 3^2$ - окружность c радиусом 3 с центром в точке $A(4;3)$

Нужно найти наибольшее значение $|z|$:

$x^2 + y^2 = |z|^2$ - окружность с центром в начале координат и радиусом $|z|$.

Эту задачу можно рассматривать как эквивалентную следующей:

Найти наибольшее значение |z|, при котором система:

$\left \{ {{(x-4)^2 + (y-3)^2 = 3^2} \atop {x^2 + y^2 = |z|^2} \right.$

Имеет решение.

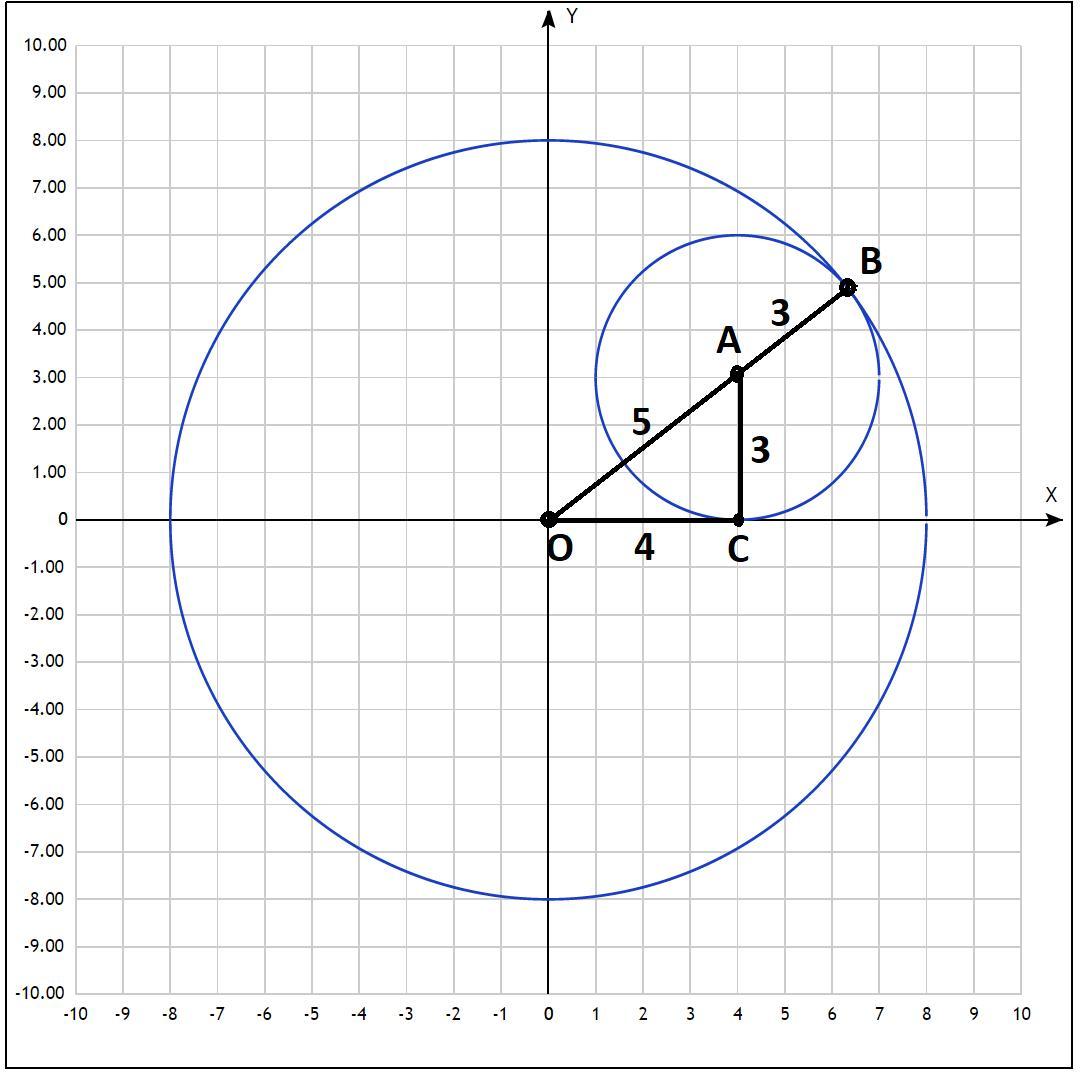
Из геометрических соображений ясно, что это произойдет, когда окружность:

$(x-4)^2 + (y-3)^2 = 3^2$

будет изнутри касаться окружности:

$x^2 + y^2 = |z|^2$

Откуда: (смотрите рисунок)

$|z|_{max} = OB = OA + AB$

Прямоугольный треугольник $OAC$ - египетский

$OA = 5\\AB = 3\\|z|_{max} = OB = 5 + 3 = 8$