Question

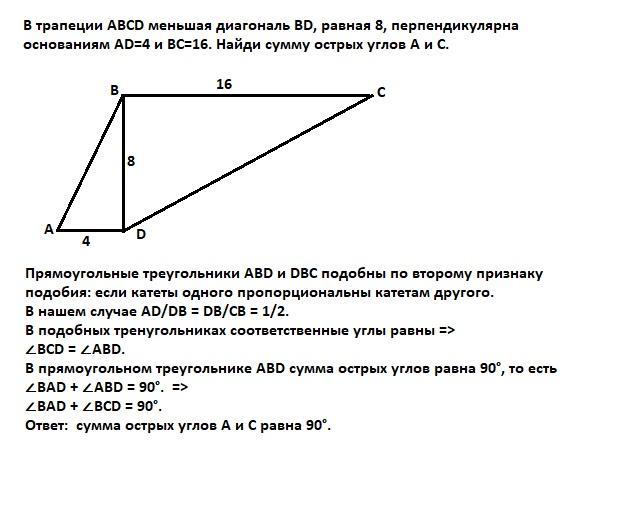
в трапеции ABCD меньшая диагональ BD равная 8, перпендикулярна основаниям AD=4 и BC=16. Найти сумму острых углов A и C.

Answer 1

Ответ:

Сумма острых углов A и C равна 90°.

Объяснение:

В трапеции ABCD меньшая диагональ BD, равная 8, перпендикулярна основаниям AD=4 и BC=16. Найди сумму острых углов A и C.

Прямоугольные треугольники ABD и DBC подобны по второму признаку: если катеты одного пропорциональны катетам другого.

В нашем случае AD/DB = DB/BC = 1/2.

В подобных треугольниках соответственные углы равны. =>

∠BCD = ∠ABD.

В прямоугольном треугольнике ABD сумма острых углов равна 90°, то есть

∠ВАD + ∠ABD = 90°  =>

∠ВАD + ∠ВСD = 90°.

Ответ: сумма острых углов A и C равна 90°.

Для любителей тригонометрии можно найти тангенсы этих углов:  

tgA = BD/AD = 8/4 = 2

tgC = BD/BC = 8/16 = 1/2.

По формуле tg(α + β) = (tgα+tgβ)/(1-tgα·tgβ) = (2+1/2)/0.

Это значит, что (α + β) = 90°.

Или так:

По Пифагору АВ = √(AD²+BD²) = 4√5.

СD = √(ВС²+BD²) = 8√5.

Sinα = AD/AB = 2√5/5. => Cosβ = 2√5/5

Sinβ = BD/CD = √5/5.  => Cosα = √5/5  

По формуле Sin(α + β) = sin(α)·cos(β) + cos(α)·sin(β) =>

Sin(α + β) = (2√5/5)·(2√5/5) + (√5/5)·(√5/5) = 4/5+1/5 = 1.

Это значит, что (α + β) = 90°.