Предмет: Алгебра,
автор: idkalmao
попалась такая задача на олимпиаде, вроде кое-что разглядел, для удобства выписал в ворд. отдаю 100 баллов тому кто объяснит как там получилось 9/4!!! НА РУССКОМ ЧУТЬ НИЖЕ!!
Приложения:

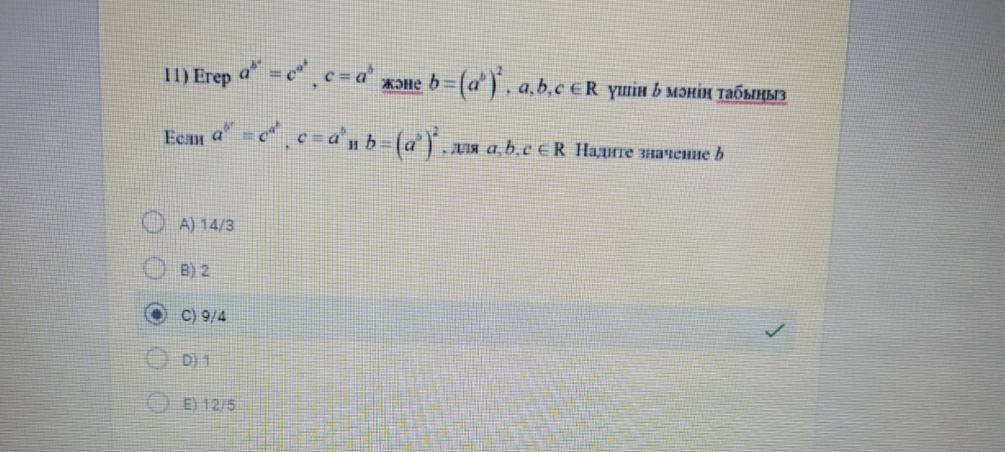
Ответы
Автор ответа:
2
Ответ: 9/4
Объяснение:
Поскольку:
, то
C учетом этого имеем:
mathgenius:
Проходили логарифмирование?
Нет. Это олимпиада 8-го класса, но в ней было столько за 9-11, что я не удивлюсь даже такому решению, но все же.. можно ли как-то иначе?:)
Наверное да
А степени с дробным показателем проходили?
3^(1/3) и прочее
a = c^(1/b)
Такой переход понимаете?
Добавил другой способ
Я попробую разобрать, это мне не на урок. Для себя прорешиваю..
спасибо
Похожие вопросы
Предмет: Русский язык,
автор: блоггер
Предмет: Русский язык,
автор: 251009
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: wholol
Предмет: Геометрия,
автор: svetaknezna