Предмет: Геометрия,
автор: maxhyrd
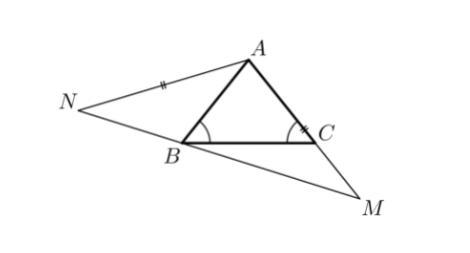
Дан равнобедренный треугольник ABC с основанием BC. На продолжении боковой стороны AC за точку C отмечена точка M. На луче MB за точкой B нашлась такая точка N, что AN=AM. Известно, что ∠CBM=24∘. Найдите угол ∠NAB.
Приложения:
cos20093:
Если провести окружность с центром в A и радиусом AB, то она где-то пересечет NM, пусть это точка F. ∠CAF - центральный угол, который в 2 раза больше ∠CBF. Точки F и B, и точки M и N симметричны относительно срединного перпендикуляра к MN => ∠NAB = ∠CAF
Ответы
Автор ответа:
11
Ответ:
48°
Объяснение:
Приложения:
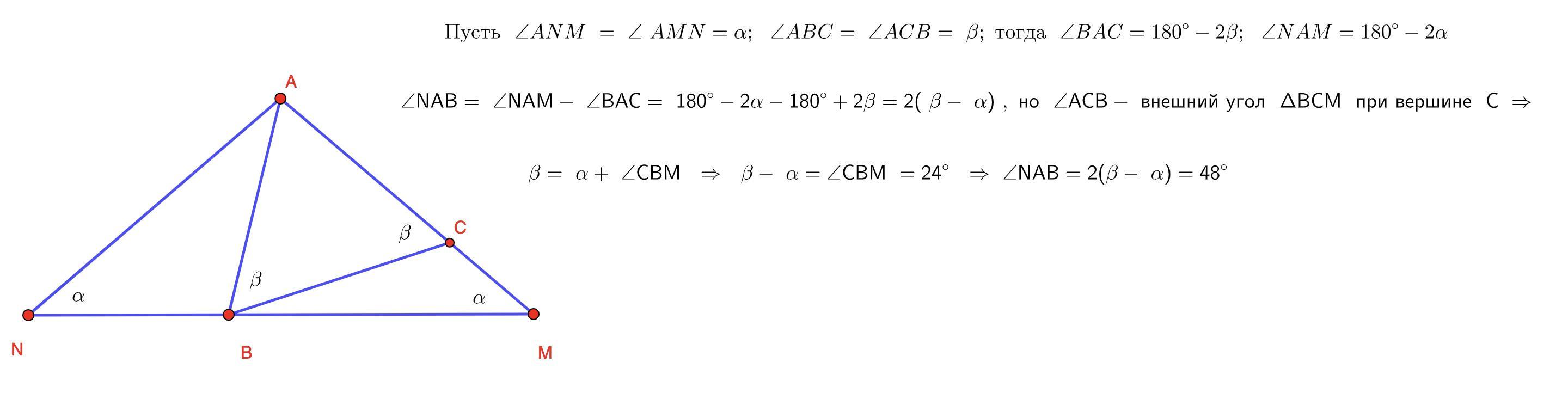
Спасибо
Автор ответа:
5
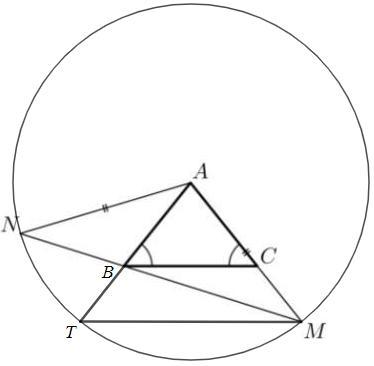
Точки N, T, M на окружности с центром A.
△TAM - р/б => △TAM~△BAC => TM||BC
∠CBM=∠BMT (накрест лежащие)
Центральный угол вдвое больше вписанного, опирающегося на ту же дугу.
∠NAT =2∠NMT =2∠CBM =48°
Приложения:
Спс
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Катюшка12356
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Окружающий мир,
автор: alserguet12345678
Предмет: Русский язык,
автор: m1lkka1