Question

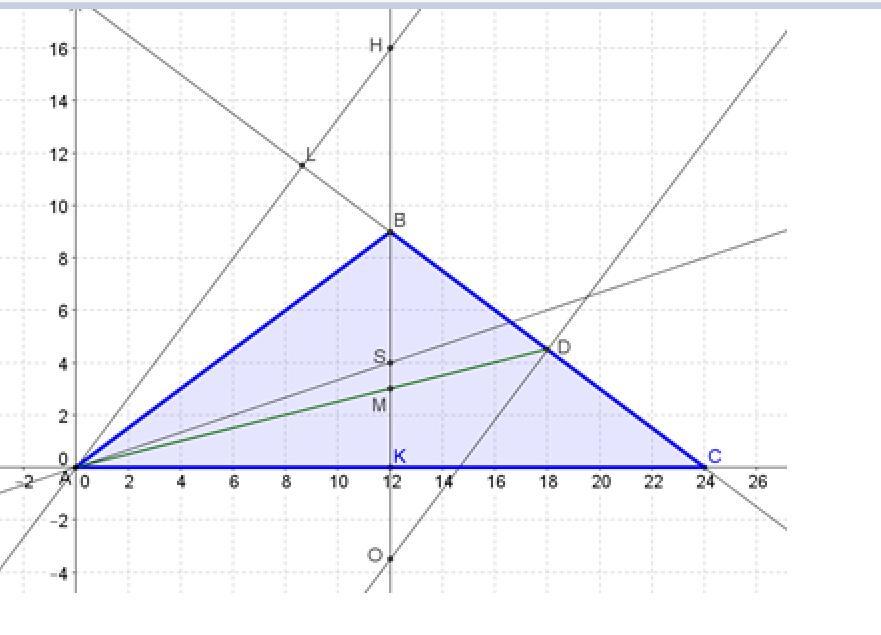
В треугольнике ABC со сторонами AB BC  15 и AC  24
найдите расстояние от вершины B до а) точки M пересечения медиан,
б) точки S пересечения биссектрис, в) центра O описанной окружности,
г) точки H пересечения высот

Answer 1

Дан треугольник ABC со сторонами AB = BC =15 и AC = 24.

Так как треугольник равнобедренный, то заданные точки в пп.а-в) лежат на высоте ВК.

Найдём её длину.

ВК = √(15² - (24/2)²) = √(225 - 144) = √81 = 9.

Найти расстояние от вершины B до

а) точки M пересечения медиан.

Используем свойство: медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины.

BM = (2/3)*9 = 6.

б) точки S пересечения биссектрис.

В треугольнике АВК точка пересечения биссектрисы со стороной ВК делит эту сторону в отношении боковых сторон.

BS/SK = 15/(24/2) = 15/12 = 5/4.

Сумма частей равна 9, тогда ВS = (9/9)*5 = 5.

в) центра O описанной окружности.

Ищем точку пересечения срединных перпендикуляров.

Из подобия взаимно перпендикулярных треугольников BOD и BKC находим: ВК/ВС = BD/BO.

Отсюда BO = ВС*BD/ВК = (15*15)/(2*9) = 25/2 = 12,5.

г) точки H пересечения высот.

Аналогично из треугольников АНК и ВСК определяем:

АК/КН = ВК/КС. Отсюда КН = АК*КС/ВК = 12*12/9 = 16.

Тогда ВН = 16 – 9 = 7.