Предмет: Геометрия,
автор: ibatulinden
Касательная к окружности в точке K параллельна хорде LM.Найдите радиус окружности, если LM=  ;KM=5. (Ответ:12,5)
;KM=5. (Ответ:12,5)
orjabinina:
Два раза т. Пифагора
Ответы
Автор ответа:
2
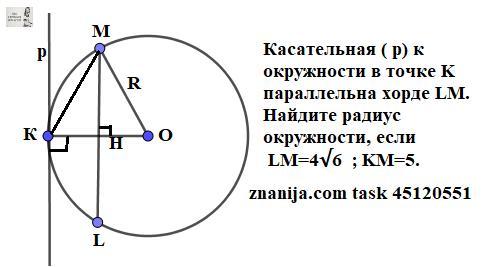
Касательная ( р) к окружности в точке K параллельна хорде LM.Найдите радиус окружности, если LM=4√6 ; KM=5. (Ответ:12,5)
Решение.
Радиус , проведенный в точку касания перпендикулярен касательной ⇒ ОК⊥р.
Т.к. р║МL , по условию , то ОК⊥МL ⇒
- ΔКМН- прямоугольный;
-радиус ОК=R делит хорду ML пополам.
По т. Пифагора для ΔКМН : КМ²=КН²+МН² , 25=КН²+(2√6)² , КН=1 ед.
Тогда НО=КО-КН=R-1.
По т. Пифагора для ΔОМН : ОМ²=MН²+ОН² ,
R²=(R-1)²+(2√6)² , R²=R²-2R+1+24 , 2R=25 , R=12,5 ед.
Приложения:
почему HO=R-1; KH=R+(R-x)=1? + что с теоремой Пифагора в KMH т.к. если расматривать на рисунке KH- высота которой вообще нету в этом треугольнике.
Насчет ho я понял, но все же поправте теорему пифагора во 2 случае т.к OM^2=MH^2+OH^2
Спасибо.
Похожие вопросы
Предмет: Английский язык,
автор: klimenkol21
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Maxim02092003
Предмет: География,
автор: AngelinaDall
Предмет: Русский язык,
автор: SVETAKIDAROVA