сторона ромба равна 16 а расстояние от точки пересечения диагоналей ромба до неё равно 4 найдите площадь ромба
Ответы
Ответ:
Площадь ромба равна 128 кв. ед.
Пошаговое объяснение:
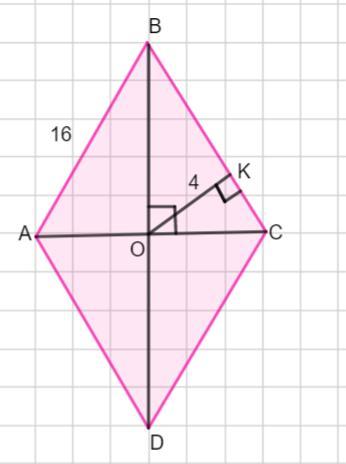
Пусть задан ромб ABCD со стороной 16 ед. Диагонали ромба пересекаются в точке О и расстояние от точки О до стороны ромба ОК= 4 ед. Надо найти площадь ромба.
Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. Тогда диагонали делят ромб на 4 равных прямоугольных треугольника и площадь ромба можно найти так: найти площадь треугольника и умножить на 4.
Рассмотрим Δ ВОС - прямоугольный. Сторона ВС =16 ед. Заданный отрезок ОК =4 ед. ОК⊥ВС и является высотой треугольника. Найдем площадь треугольника как полупроизведение стороны на высоту, проведенную к этой стороне
Площадь треугольника равна 32 кв. ед. Тогда площадь ромба в 4 раза больше
(кв. ед.)
Значит, площадь ромба равна 128 кв. ед.
#SPJ3