То что предела нет я знаю но нужно это доказать. Прошу развернутое доказательство все таки даю 100 балов
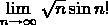
Ответы
Відповідь:
Функция sqrt (n) × sin (n!) при n стремящемся к бесконечности является не определенной.
Покрокове пояснення:
Предел функции sqrt (n) × sin (n!) при n стремящемся к бесконечности состоит из двух множителей:
1) множитель sqrt (n) стремится к бесконечности при n стремящемся к бесконечности;
2) множитель sin (n!) - имеет не определенный предел на бесконечности.
Следовательно и вся функция sqrt (n) × sin (n!) при n стремящемся к бесконечности является не определенной.
Докажем это на примере функции sin (n), которая имеет так же ведет себя как и функция sin (n!) при n стремящемся к бесконечности.
Рассмотрим предел функции sin (n) при n стремящемся к бесконечности. Функция sin - знакопериодичная, так, что ее предел на бесконечности является не определенным.
Докажем это методом от противного. Пусть предел функции sin (n) при n стремящемся к бесконечности существует, значит есть конечное число, которое является решением этого предела.
Тогда предел при n стремящемся к бесконечности для функции
( sin (n+1) - sin (n-1) ) = 0
Применим формулу разности двух синусов.
sin (A) - sin (B) = 2 × cos ((A+B)/2) × sin ((A-B)/2)
Получается, что предел при n стремящемся к бесконечности для функции
2 × cos (n) × sin (1) = 0
Следовательно предел функции cos (n) = 0 при n стремящемся к бесконечности.
Значит предел при n стремящемся к бесконечности для функции
sin (2n) = 2 × sin (n) × cos (n) = 0.
Но тогда если предел sin (n) при n стремящемся к бесконечности существует, то он равен нулю.
Также всегда должно выполняться основное тригонометрическое тождество sin^2(n) + cos^2(n) = 1.
Это значит, что cos(n) стремится к нулю, а sin(n) стремится в единице.
Это противоречит здравому смыслу, значит предел функции sin (n) при n стремящемся к бесконечности является не определенным.