Question

№10. Укажите промежуток, которому принадлежит корень уравнения $\sqrt{x+12}=3.$
А) [-12; -6);
Б) [-6; 0);
В) [0; 6);
Г) [6; 12);
Д) [12; +∞).

Answer 1

Ответ:

Б

Объяснение:

$\sqrt{x+12}=3$

По определению арифметического квадратного корня

$3^2=x+12\\x+12=9\\x=9-12\\x=-3$

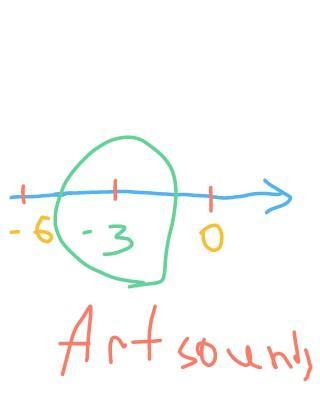
Корень -3 принадлежит промежутку [-6; 0), так как он больше -6, но меньше 0.

Answer 2

Ответ:

$\sqrt{x + 12} = 3 \\ \sqrt{x + 12} {}^{2} = 3 {}^{2} \\ x + 12 = 9 \\ x = 9 - 12 \\ x = - 3 \\ - - - - - - - - - \\ \sqrt{( - 3) + 12} = 3 \\ \sqrt{9} = 3 \\ 3 = 3$

Следовательно, « -3 » проходит через промежуток : « -6; 0 »

--------------

Ответ : Б)