При каком наибольшем значении параметра a уравнение  имеет ровно один корень?
имеет ровно один корень?
Ответы
Ответ: а=24 .
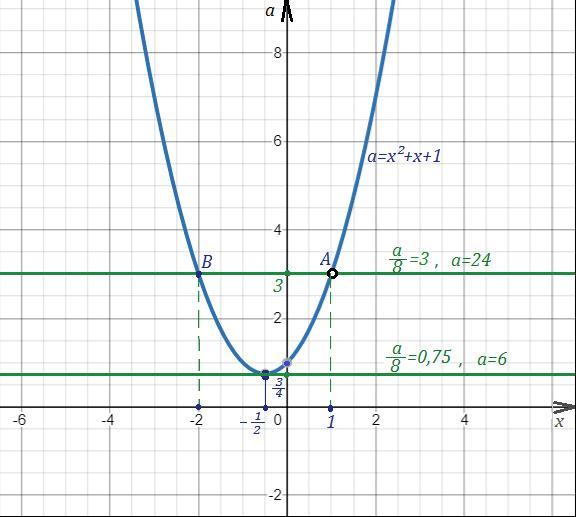
Строим параболу и проводим прямую
.
Парабола имеет вершину в точке .
При х=1 квадратный трёхчлен принимает значение
.
Значит, на графике параболы надо выколоть точку А(1;3) .
Прямые вида параллельны оси ОХ и проходят через точки, ординаты которых равны
. Так как точка (1;3) не принадлежит параболе, то прямая, параллельная оси ОХ и проходящая через точку с ординатой у=3, будет пересекать параболу не в двух, а только в одной точке с координатами В(-2;3) .
Ещё один раз прямая, параллельная оси ОХ, пересечёт параболу лишь в её вершине , то есть при .
Итак при и при
прямая, параллельная
оси ОХ, пересечёт параболу один раз.
Наибольшим значением параметра будет значение а=24 ( значение
а=6 - наименьшее значение ).