Предмет: Математика,
автор: imn2002114
Нужно решить пример по математике
Приложения:
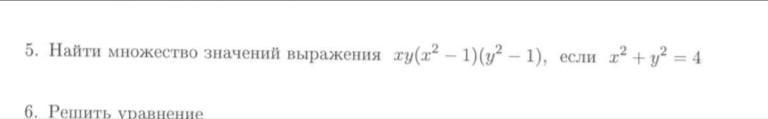
Ответы
Автор ответа:
1
где
Дальше элементарное исследование функции с помощью производной.
f(-2)=-2; f(2)=2. Вывод: множество значений функции - это отрезок [-2;2].
imn2002114:
подскажите, вы через какую-то программу это решали?
Латекс
Решал, естественно, сам, а в написании формул использовал LATEX, используемый на этом сайте.
Спасибо ща информацию
Похожие вопросы
Предмет: Русский язык,
автор: arinakr
Предмет: Русский язык,
автор: lizakiy
Предмет: Другие предметы,
автор: оксанаОо
Предмет: Алгебра,
автор: IGORG2003
Предмет: Алгебра,
автор: arinamm0611