Предмет: Алгебра,
автор: laatakroft
Для каждого параметра a решите систему уравнений
Приложения:
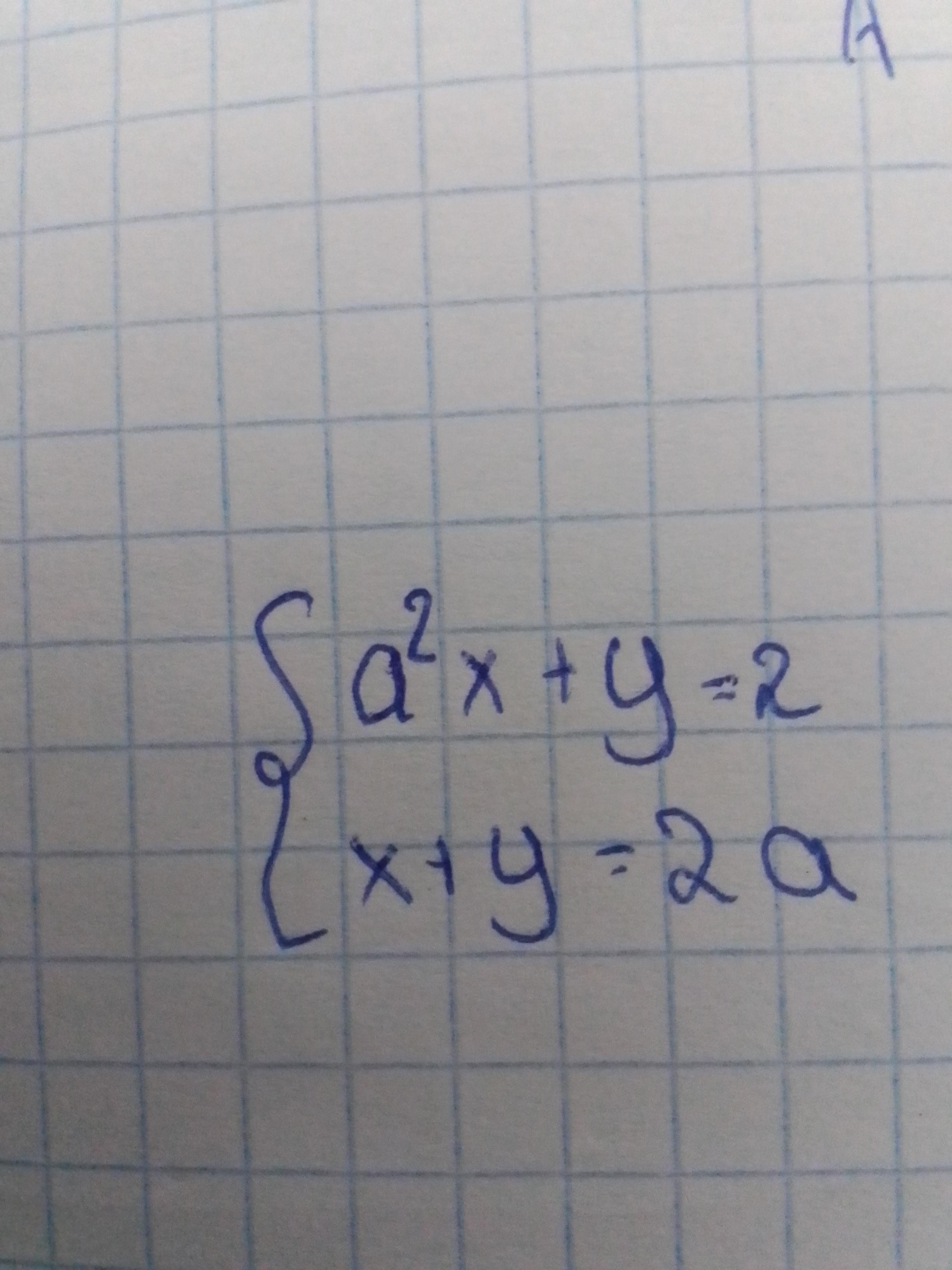
Mixassm:
Так какие конкретно параметры а? Их может быть бесконечно много
не хватает информации о том, какие именно параметры "а", так как чисел бесконечное количество
По условию систему необходимо решить для каждого возможного значения параметра а. Условие полно и корректно (единственное - пропущено слово "значения" после слова "каждого"). Параметров а бесконечно много, но на возможность нахождения решения это не влияет.
а!=-1
Ответы
Автор ответа:
0
{ a^2*x + y = 2
{ x + y = 2a
Выразим y через x в обоих уравнениях:
{ y = 2 - a^2*x
{ y = 2a - x
Приравняем правые части:
2 - a^2*x = 2a - x
2 - 2a = a^2*x - x
-2(a - 1) = x(a^2 - 1) = x(a - 1)(a + 1)
При a = 1 обе части равны 0, x может быть любым, а y = 2a - x = 2 - x
При a не = 1 сокращаем (a - 1)
-2 = x(a + 1)
x = -2/(a + 1)
При a = -1 решений нет, при a не = -1 решение единственное:
x = -2/(a + 1)
y = 2a - x = 2a + 2/(a + 1) = (2a(a+1) + 2)/(a + 1) = (2a^2 + 2a + 2)/(a + 1)
Ответ:
При a = 1: x ∈ (-oo; +oo); y = 2 - x
При a = -1 решений нет.
При всех остальных а: x = -2/(a + 1); y = (2a^2 + 2a + 2)/(a + 1)
Только немного поправить: при а=1 x и y не совсем любые. Их сумма все ещё должна равняться 2
Согласен
Похожие вопросы
Предмет: Українська мова,
автор: sashafedorenko4
Предмет: Русский язык,
автор: проспоммптр
Предмет: Қазақ тiлi,
автор: Anelia111
Предмет: Математика,
автор: 5SashaRyskin5
Предмет: Математика,
автор: мая107