Предмет: Математика,
автор: nimurafuruta1
Помогите решить, пожалуйста
Приложения:
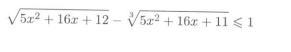
Ответы
Автор ответа:
1
Ответ:
(см. объяснение)
Пошаговое объяснение:
Пусть . Тогда
.
Пусть . Тогда
.
Получили систему:
Выразим из второй ее строки:
Подставим в первую:
Домножим записанное выше на . Причем то, на что мы домножаем точно не является отрицательным числом, поэтому знак неравенства сохранится. Несложно понять, что написанное ниже равносильно тому, что находится выше.
Получили неравенство относительно одной переменной .
Причем решить его не составляет труда:
Делаем обратную замену:
Возводим все в куб:
Получили простейшие уравнение и двойное неравенство.
Решая каждую строку совокупности и объединяя вычисленное, получаем ответ:
Неравенство решено!
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: muradim20062
Предмет: Русский язык,
автор: Anechka236
Предмет: Физика,
автор: даня1270