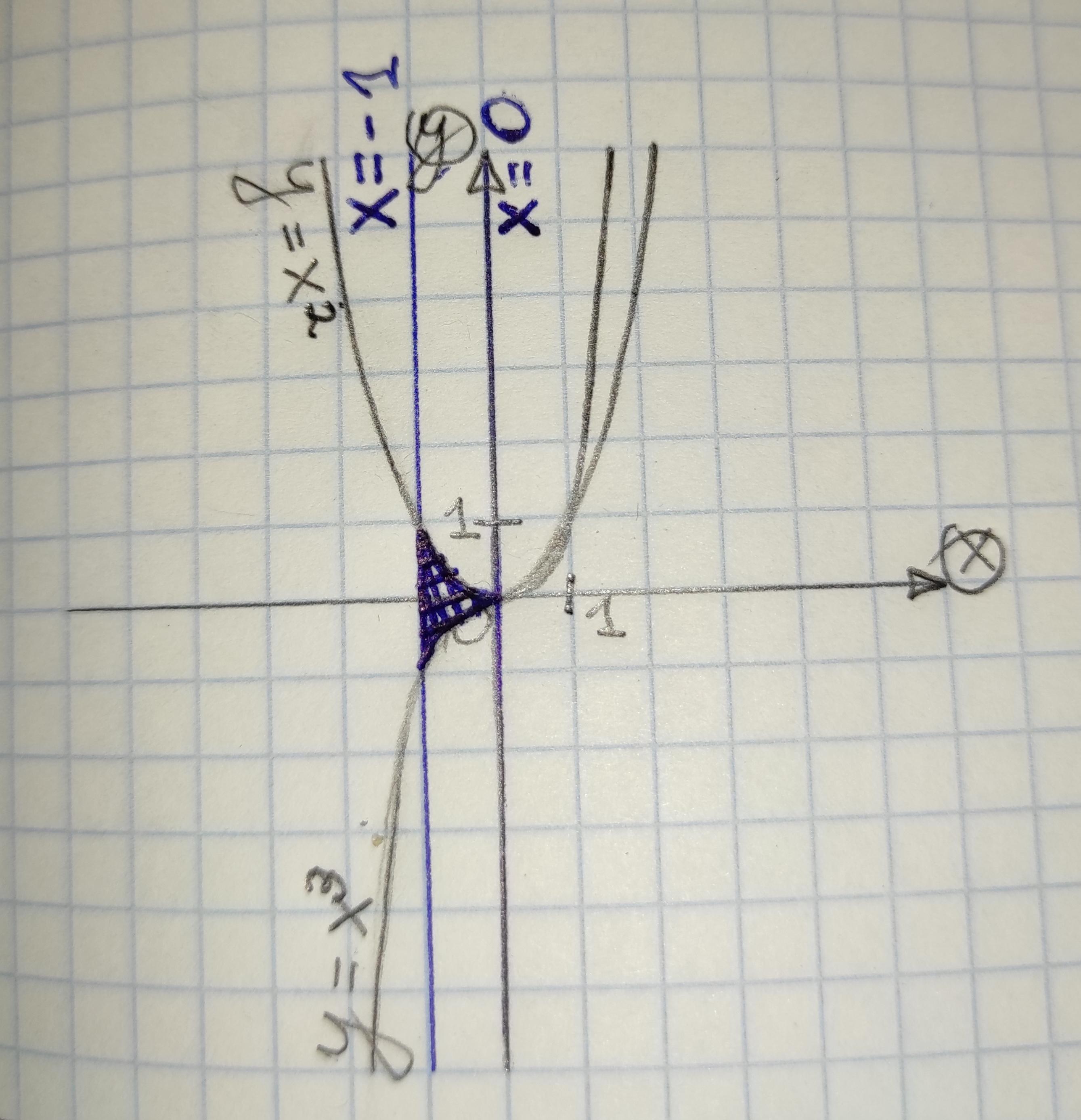
Сделайте чертеж и вычислите площадь фигуры, ограниченной линиями:
Дай бог здоровья кто это решит \:
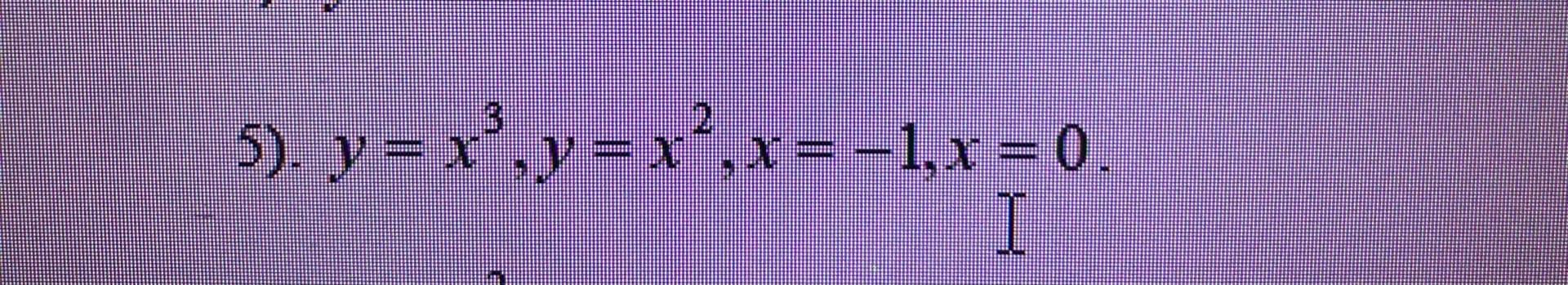
Ответы
Ответ:
Объяснение:
формула для вычисления
когда сделаем чертеж, увидим, что пределы интегрирования b=-1, a=0
за у₁ принимают функцию, график которой лежит "выше", у на это
у₁ = х², тогда у₂ = х³
вот, всё у нас есть, считаем площадь
Ответ:
7/12
Объяснение:
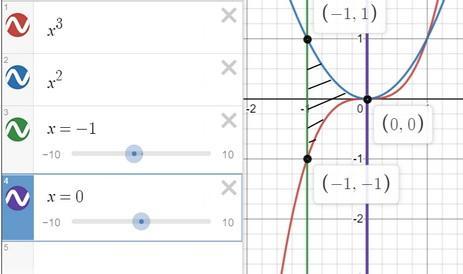
Заштрихованная фигура состоит из двух криволинейных трапеций. Одна, находящаяся над осью абсцисс, ограничена графиком y = x², двумя вертикальными прямыми x = -1 и x = 0, а также самой осью Ox. Вторая, находящаяся под осью абсцисс (из-за этого ее площадь возьмем со знаком минус), ограничена графиком y = x³, теми же вертикальными прямыми и той же осью Ox.
Тогда площадь S рассматриваемой фигуры будет равна сумме двух определенных интегралов (один — от x², другой — от x³ со знаком минус), оба вычисленных на отрезке [-1; 0]: