Предмет: Математика,
автор: kainovdima37088
Решите уравнение.
Пожалуйста подробно!
Приложения:
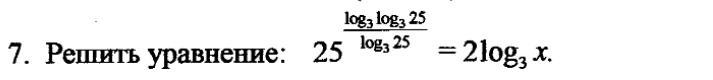
orjabinina:
x=5 , вроде
Ответы
Автор ответа:
0
Ответ:
(см. объяснение)
Пошаговое объяснение:
Заметим, что:
Тогда:
Данный корень удовлетворяет условию .
Задание выполнено!
Простите,я немного не понял,как мы всё преобразовали в log3(25).
Можете объяснить пожалуйста
Можете объяснить пожалуйста
Автор ответа:
1
=
, ограничения х>0
По правилу преобразуем степень числа 25.
Получим .
По основному логарифмическому тождеству( есть в инете)
.
Тогда уравнение примет вид =
,
=
,
=
,
=
,
x=5, 5>0
Ответ х=5
Все ясно?
Похожие вопросы
Предмет: Английский язык,
автор: Марк1111111111111
Предмет: Русский язык,
автор: Лунтикдалбан
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: yurdum85
Предмет: Химия,
автор: tatyana7895