Предмет: Геометрия,
автор: skaras1996
Сегодня БЫЛА (уже прошла) олимпиада, я не справилась с задачей: В прямоугольнике ABCD с большей стороной AD точка E — середина стороны AB, a M — основание перпендикуляра, опущенного из вершины D на отрезок CE. Докажите, что треугольник MAD — равнобедренный.
Объясните, если кто понимает.... по времени ...теперь)))...не горит, просто хочется разобраться.
Ответы
Автор ответа:
0
Проведем ЕК параллелльно АД.
Углы ВЕС и ЕСК равны как накрестлежащие при параллельных ВЕ и СК
Рассмотрим прямоугольные треугольники ВЕС и ДМС.
Они подобны, т.к. если в одном прямоугольном треугольнике один из острых углов равен острому углу другого, то эти треугольники подобны
Следовательно, углы ВСЕ и МДС равны.
Опустим из Е перпендикуляр ЕН на АС, и проведем НТ параллельно ЕМ.
Получился прямоугольник МЕНТ
В прямоугольнике ВСКЕ углы ВСЕ и СЕК равны как накрестлежащие при параллельных ВЕ и СК.
В прямоугольнике ЕМТН НМ и ЕТ - диагонали.
Они равны и точкой пересечения О делятся пополам.
Следовательно, треугольник ЕМО равнобедренный, и угол МЕТ равен углу ЕМН.
А так как угол СЕК и МЕТ - один и тот же, угол ЕМА равен углу ВСЕ и равен углу СДМ.
Каждый из этих равных углов дополняет углы при МД до прямого.
Следовательно, углы АМД и АДМ равны, и треугольник АМД - равнобедренный.
Углы ВЕС и ЕСК равны как накрестлежащие при параллельных ВЕ и СК
Рассмотрим прямоугольные треугольники ВЕС и ДМС.
Они подобны, т.к. если в одном прямоугольном треугольнике один из острых углов равен острому углу другого, то эти треугольники подобны
Следовательно, углы ВСЕ и МДС равны.
Опустим из Е перпендикуляр ЕН на АС, и проведем НТ параллельно ЕМ.
Получился прямоугольник МЕНТ
В прямоугольнике ВСКЕ углы ВСЕ и СЕК равны как накрестлежащие при параллельных ВЕ и СК.
В прямоугольнике ЕМТН НМ и ЕТ - диагонали.
Они равны и точкой пересечения О делятся пополам.
Следовательно, треугольник ЕМО равнобедренный, и угол МЕТ равен углу ЕМН.
А так как угол СЕК и МЕТ - один и тот же, угол ЕМА равен углу ВСЕ и равен углу СДМ.
Каждый из этих равных углов дополняет углы при МД до прямого.
Следовательно, углы АМД и АДМ равны, и треугольник АМД - равнобедренный.
Приложения:
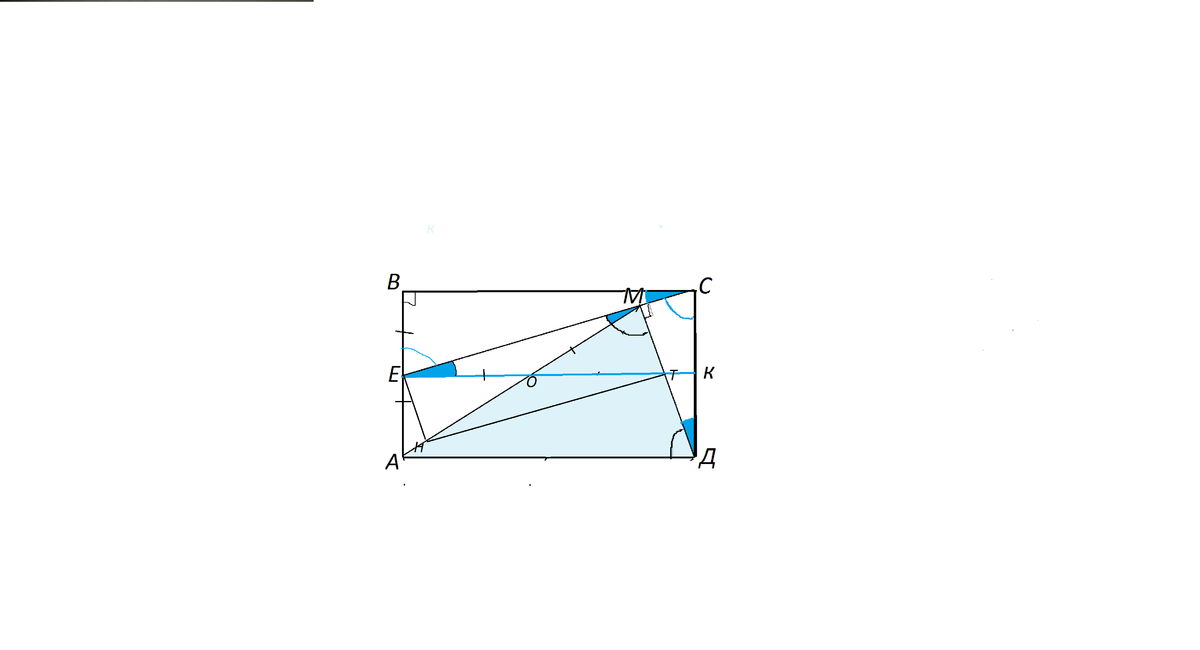
Автор ответа:
0
Вы правы, упустила. Надо додумать, как это доказать. В противном случае ответ удалю.
Автор ответа:
0
Вы правы, немного поспешила, показалось очевидным это равенство. Ответ дополнила, надеюсь, теперь решение верное.
Похожие вопросы