Question

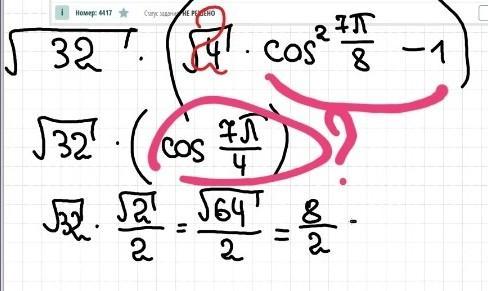
куда он это убрал? почему cos² вдруг стало просто cos?, а куда ушло -1? cos²45 разве не cos(45)²?странно...ну да ладно ...но вот минус 1 куда ушло?​

Answer 1

$\sqrt{32}\cdot\Big(\sqrt{4}\cdot Cos^{2} \dfrac{7\pi }{8} -1\Big)=\sqrt{16\cdot 2}\cdot \underbrace{\Big(2Cos^{2}\dfrac{7\pi }{8}-1\Big)}_{Cos\Big(2\cdot \dfrac{7\pi }{8}\Big)}=4\sqrt{2}\cdot Cos\dfrac{7\pi }{4}=\\\\=4\sqrt{2}\cdot Cos\Big(2\pi-\dfrac{\pi }{4})=4\sqrt{2}\cdot Cos\dfrac{\pi }{4}=4\sqrt{2}\cdot\dfrac{\sqrt{2} }{2}=\dfrac{4\cdot 2}{2}=\boxed4$

При решении  прменены формулы :

1) косинуса двойного угла :

$2Cos^{2}x-1=Cos2x$

2) формулы приведения :

$Cos\Big(2\pi-x)=Cosx$

$4291)\sqrt{32}-\sqrt{128}Sin^{2}\dfrac{9\pi }{8} =\sqrt{16\cdot 2} -\sqrt{64\cdot 2}\cdot Sin^{2} \Big(\pi +\dfrac{\pi }{8}\Big)=\\\\=4\sqrt{2}-8\sqrt{2}\cdot \underbrace{Sin^{2}\dfrac{\pi }{8}}_{\dfrac{1-Cos\frac{\pi }{4} }{2}} =4\sqrt{2}-8\sqrt{2}\cdot \dfrac{1-Cos\frac{\pi }{4} }{2}=\\\\=4\sqrt{2}-4\sqrt{2}\cdot \Big(1-\dfrac{\sqrt{2} }{2}\Big)=4\sqrt{2}-4\sqrt{2}+4=\boxed4$