Сколько треугольников на рисунке ?

Ответы
Відповідь:
216 треугольников.
Покрокове пояснення:
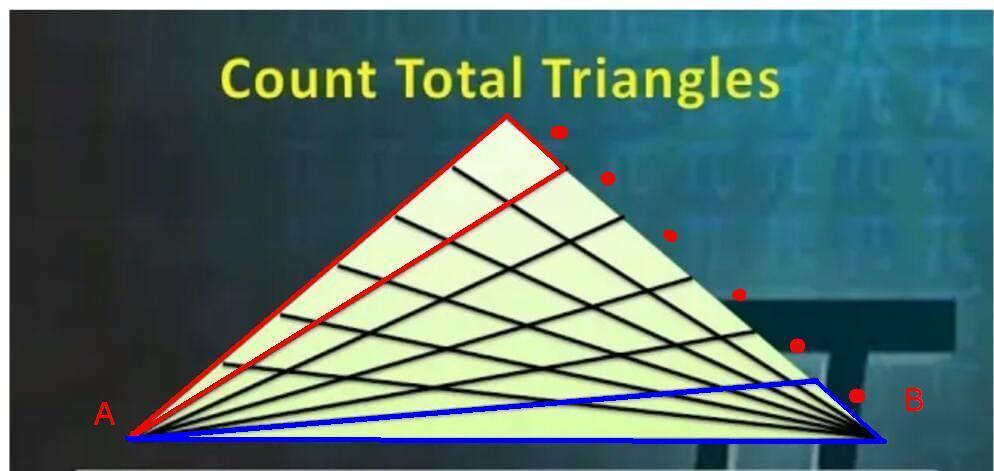
На 1 рисунке в красном треугольнике ( вершина в точке А ) с стороной противолежащей вершине А равной 1 единице находится 6 треугольников, таких треугольников может быть 6 штук ( отмечены точками ). Всего 6 × 6 = 36 треугольников. Аналогичным образом можно построить треугольники с вершиной в точке В. Их будет 6 × 5 = 30 треугольников ( 6 треугольников вошли в 36 с вершиной в точке А ). Итого:
6 × ( 6 + 5 ) треугольников.
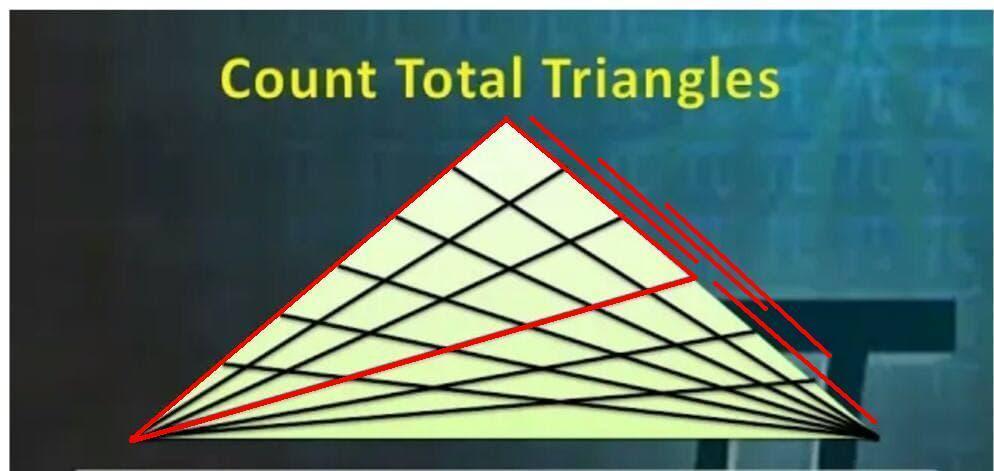
На рисунке 2 проведем аналогичный подсчет числа треугольников:
6 × ( 5 + 4 ) треугольников.
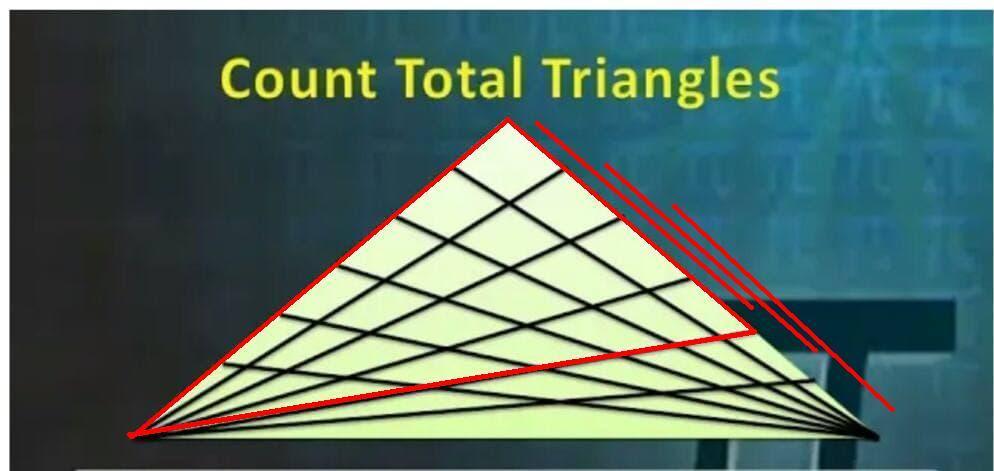
Рисунок 3:
6 × ( 4 + 3 ) треугольников.
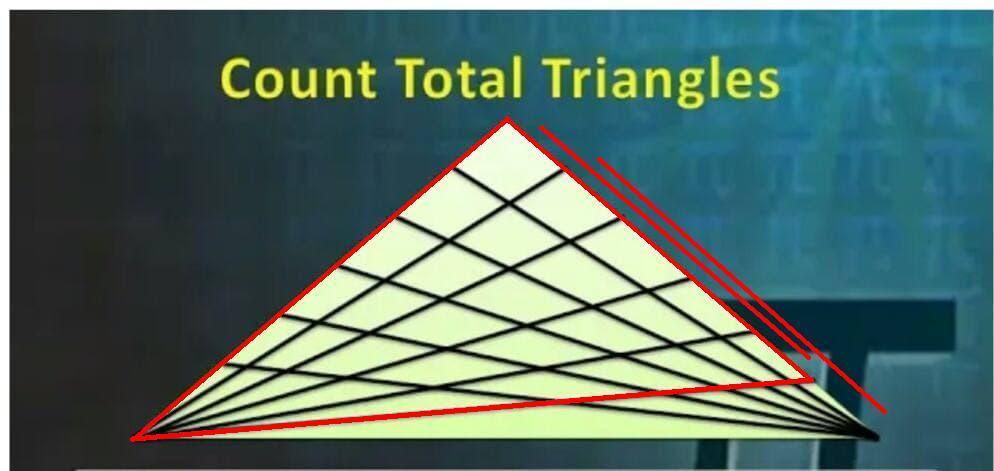
Рисунок 4:
6 × ( 3 + 2 ) треугольников.
Рисунок 5:
6 × ( 2 + 1 ) треугольников.
И последний вариант ( сайт не позволяет загрузить больше 5 рисунков ) - 6 треугольников со стороной противолежащей вершине А равной 6 единицам, аналогичные треугольники, построенные с вершиной в точке В - учтены ранее.
Всего:
6 × ( 11 + 9 + 7 + 5 + 3 + 1 ) = 216 треугольников.

Ответ: 241
Пошаговое объяснение:
В комментарии уже писал, но все же распишу сам принцип нахождения.
Ну, хотя бы больше не последует ненужных спам-ответов.
Выводить формулу буду не для данного треугольника, а для произвольного треугольника, из вершин A и B (как на рисунке) которого, выходит по n прямых. (в нашем случае n = 6, а самую нижнюю прямую в основании мы не рассматриваем).
Нетрудно убедится, что все треугольники, что есть на рисунке cодержат либо вершину A, либо вершину B.
Найдем число треугольников, что содержит вершину A.
Рассмотрим n прямых и прямую в основании, выходящие из вершины A.
Всего n+1 прямых.
Число треугольников, образованных этими n+1 прямыми и прямой BC равно C(2,n+1) - число сочетаний из n+1 элементов по 2.
C(2, n+1) = n(n+1)/2
Через каждый треугольник из данного множества проходит n прямых выходящих из вершины B, откуда общее число треугольников содержащих вершину A равно:
n^2(n+1)/2
Тоже самое число треугольников содержит вершину B ( из симметрии).
Но существуют треугольники, что содержат обе вершины A и B, число таких треугольников равно числу точек пересечения n прямых выходящих из вершины A и n прямых выходящих из вершины B.
Число таких треугольников равно: n^2
Откуда, общее число треугольников на рисунке:
N = 2*n^2(n+1)/2 - n^2 = n^3 + n^2 -n^2 = n^3
В нашем случае, n = 6
N(6) = 6^3 = 216
Но более внимательные решающие, могут заметить еще треугольники на этом рисунке.
Один из треугольников я отметил цифрой 1.
Но это еще не все!
Есть еще треугольники на заднем плане, которые очень труднозаметны!
Число таких треугольников считается по уже известному принципу:
C(2,4)*4 = 3*4/2 *4 = 24
Тогда общее число треугольников:
216 + 25 = 241 !
