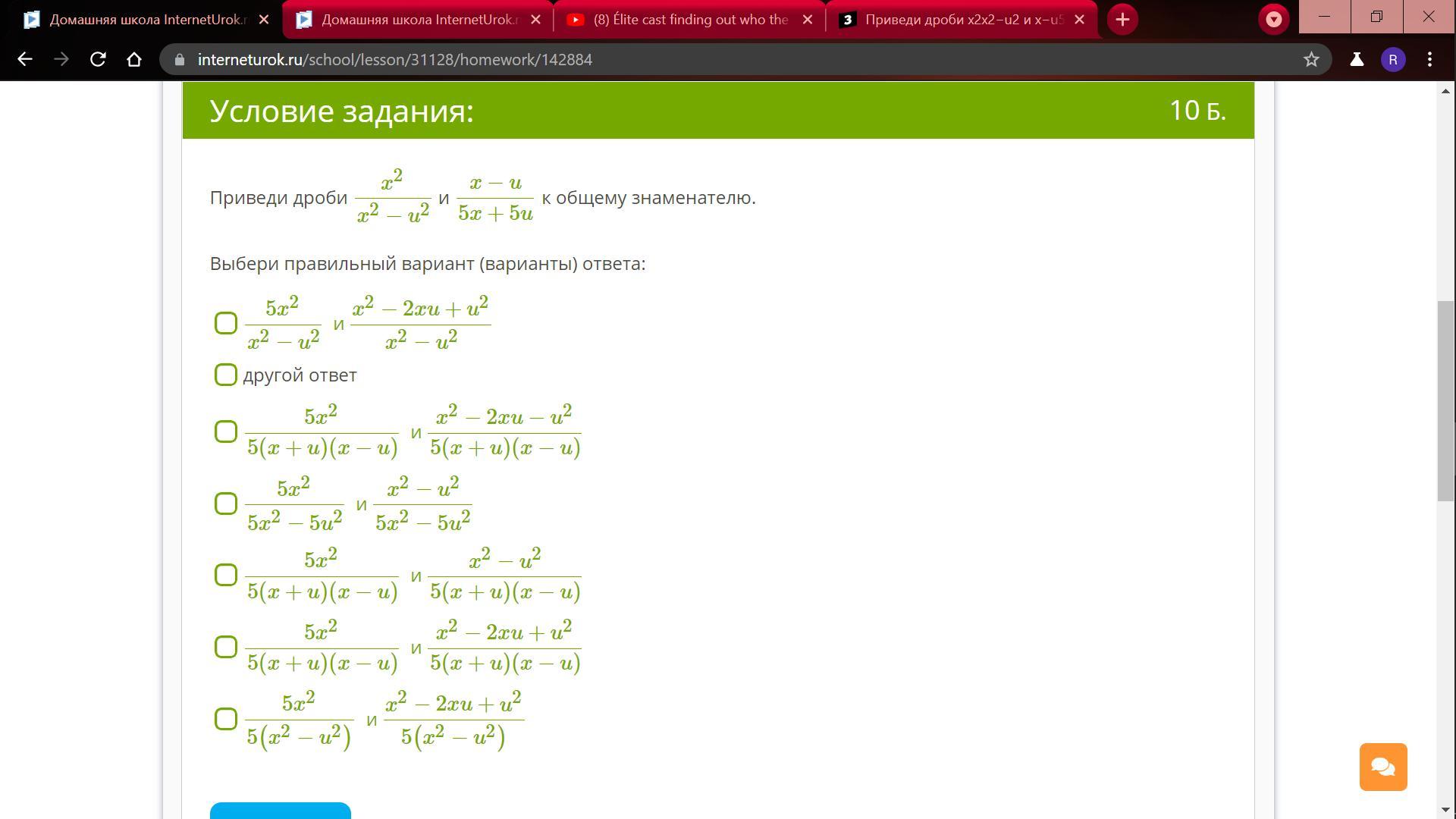
Приведи дроби x2x2−u2 и x−u5x+5u к общему знаменателю.
Выбери правильный вариант (варианты) ответа:
5x2x2−u2 иx2−2xu+u2x2−u2
другой ответ
5x25(x+u)(x−u) иx2−2xu−u25(x+u)(x−u)
5x25x2−5u2 иx2−u25x2−5u2
5x25(x+u)(x−u) иx2−u25(x+u)(x−u)
5x25(x+u)(x−u) иx2−2xu+u25(x+u)(x−u)
5x25(x2−u2) иx2−2xu+u25(x2−u2)
Ответы
Ответ:
6,7
Объяснение:
x²/(x² - u²) и (x - u)/(5x +5u)
x² / (x - u)(x + u) ↔ (x - u) / 5(x + u)
x² * 5 /5* (x - u)(x + u) и (x - u)*(x - u) / 5(x + u)(x - u)
5x² / 5* (x - u)(x + u) и (x - u)² / 5(x + u)(x - u)
5x² / 5(x - u)(x + u ) и (x² -2xu +u²) / 5(x - u)(x + u ) - ответ 6 (предпоследний)
5x² / 5(x² - u²) и (x² -2xu +u²) / 5(x² - u²) - ответ 7 (последний)
Ответ:
6,7) 5x²/(5(x-u)(x+u)) и x²-2xu+u²/(5(x-u)(x+u))
Объяснение:
знаменатель первой дроби представить в другом виде, воспользовавшись формулой разность квадратов: (x-u)(x+u)
у знаменателя второй дроби вынести общий множитель: 5(x+u)
⇒ общий знаменатель 5(x-u)(x+u) = 5(х²-u²) = 5x²-5u²
⇒⇒ числитель первой дроби умножить на 5, а числитель второй дроби на (х-u)
5x² и (х-u)(x-u) === 5x² и (х-u)² === 5x² и x²-2xu+u² (это формула квадрат разности)