Question

ГЕОМЕТРИЯ ОЧЕНТ СРОЧНО МОЛЮЮЮ

Answer 1

Ответ:

1)

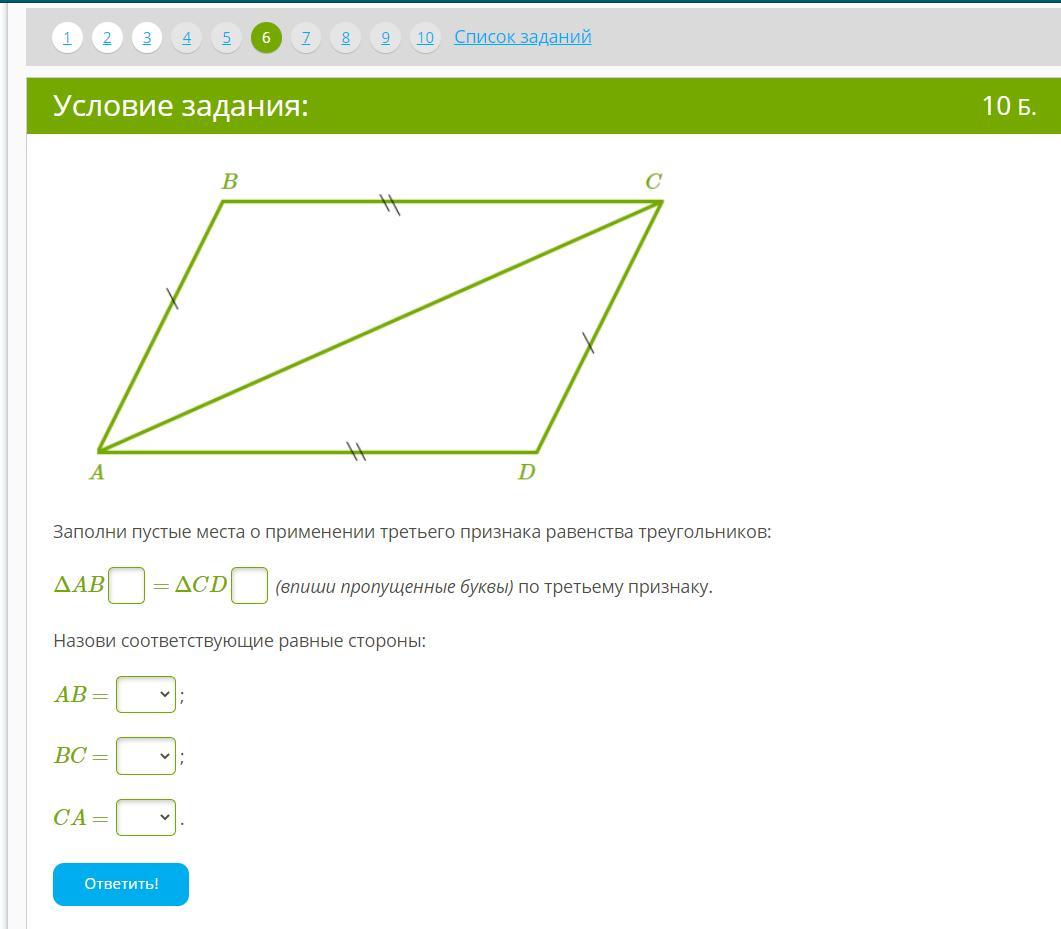
ΔABC = ΔCDA;

AB = CD;

BC = AD;

CA = AC.

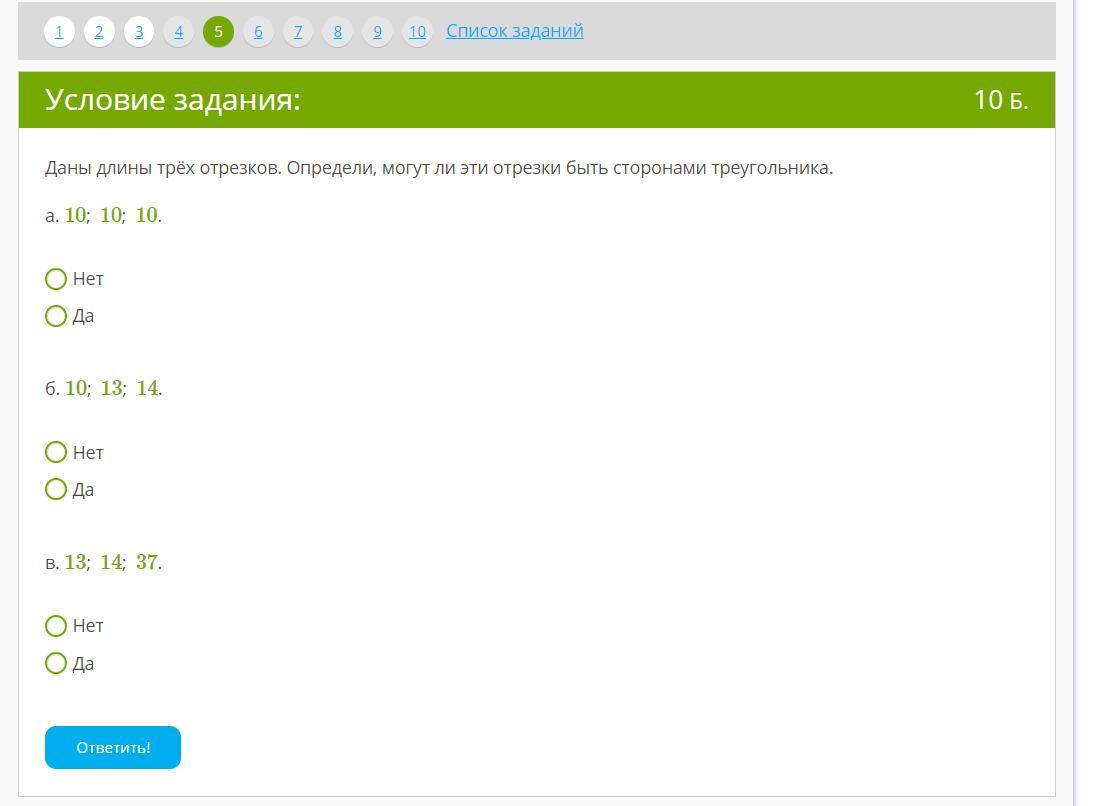
2) Чтобы узнать могут ли быть числа сторонами треугольника, надо сложить длины двух наименьших сторон и если их сумма равна или меньше длины наибольшей стороны то треугольник не получится.

A) 10 + 10 > 10

20 > 10

Да.

Б) 10 + 13 > 14

23 > 14

Да.

В) 13 + 14 < 37

27 < 37

Нет.

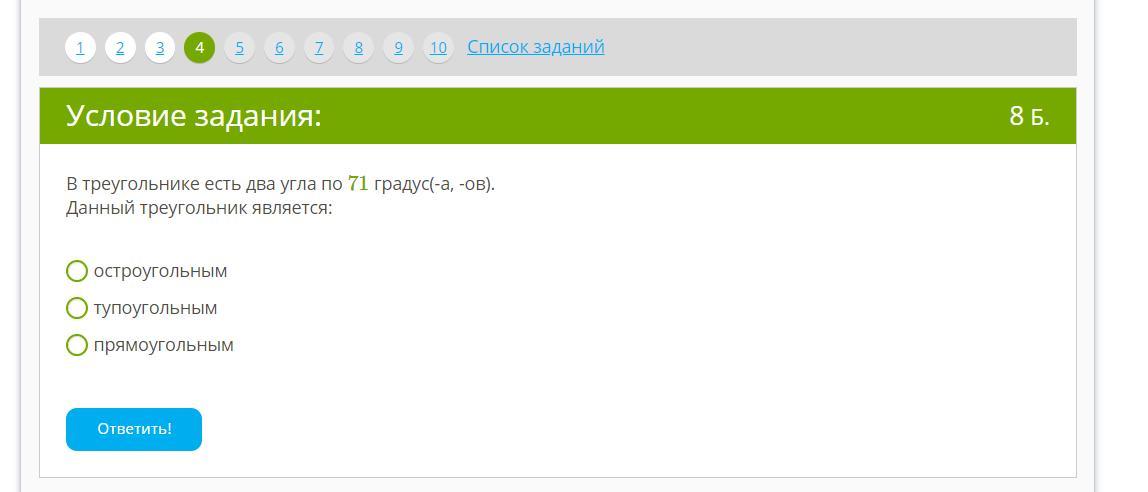
3) Данный треугольник является остроугольным.

Answer 2

Объяснение объяснения

ЗАДАЧА С ПАРАЛЛЕЛОГРАММОМ:

∆АВС=∆СДА – по 3-му признаку (по 3-м сторонам):

АВ=СД – по условию

ВС=АД – по условию

СА – общая сторона

ЗАДАЧА 2( с треугольником)

Сумма двух любых сторон треугольника всегда больше одной из них, проверим данные варианты:

1) 10, 10, 10

Во-первых в равностороннем треугольнике все стороны равны и эти отрезки могут быть его сторонами

10+10=20

20 > 10 – так же подходит по сумме сторон

ВЫВОД: ДА, эти отрезки могут быть сторонами треугольника

2) 10; 13; 14

10+13=23 => 23 > 14

10+14=24 => 24 > 13

13+14=27 => 27 > 10

ВЫВОД: ДА, эти отрезки могут быть сторонами треугольника

3) 13; 14; 37

13+14=27 => 27 < 37

ВЫВОД: НЕТ, эти отрезки не могут быть сторонами треугольника, поскольку одна сторона больше суммы двух других сторон.

ЗАДАЧА 3

Сумма углов треугольника составляет 180°, и если каждый из 2 данных углов равен 71°, то 3-й угол составит:

180–71–71=38°

Этот треугольник остроугольный, поскольку острый угол всегда меньше 90°: 71°; 71°, 38°