Предмет: Математика,
автор: sonya290299
СРОЧНО!!!!!Применяя правило лопиталя, вычислить
Приложения:
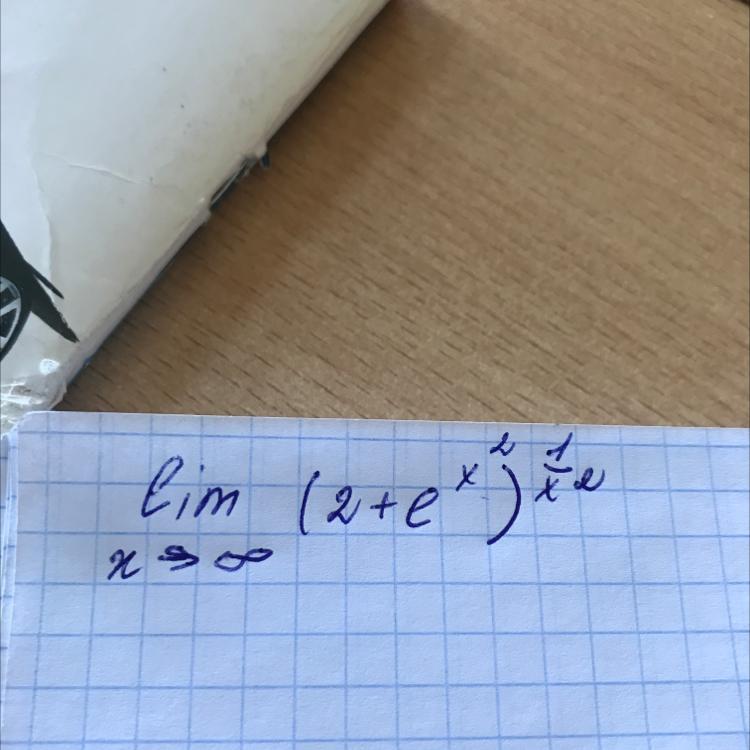
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
В силу непрерывности функции имеем
Значит,
Похожие вопросы
Предмет: Русский язык,
автор: nail200617
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: alkhas
Предмет: Математика,
автор: haydarkan2004