Предмет: Математика,
автор: vladgamer995
розв'язати систему рівнянь
Приложения:
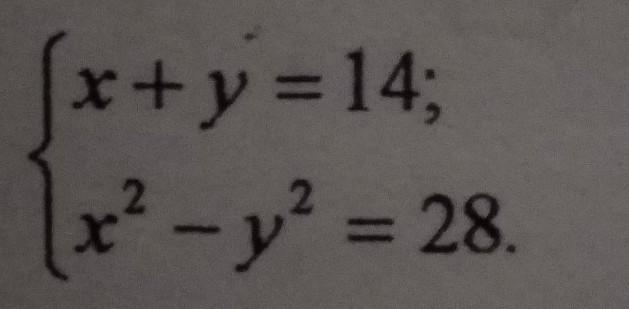
Ответы
Автор ответа:
2
Автор ответа:
1
Ответ:
.
Пошаговое объяснение:
Виразимо змінну x через y з першого рівняння:
Підставимо значення x в друге рівняння:
Підставимо знайдене значення y в перше рівняння:
Перевіримо знайдені значення x і y:
Система рівнянь розв'язана!
Похожие вопросы
Предмет: Английский язык,
автор: викуся315
Предмет: Русский язык,
автор: Gafurjan
Предмет: Русский язык,
автор: galinacyzz
Предмет: Геометрия,
автор: id187850377