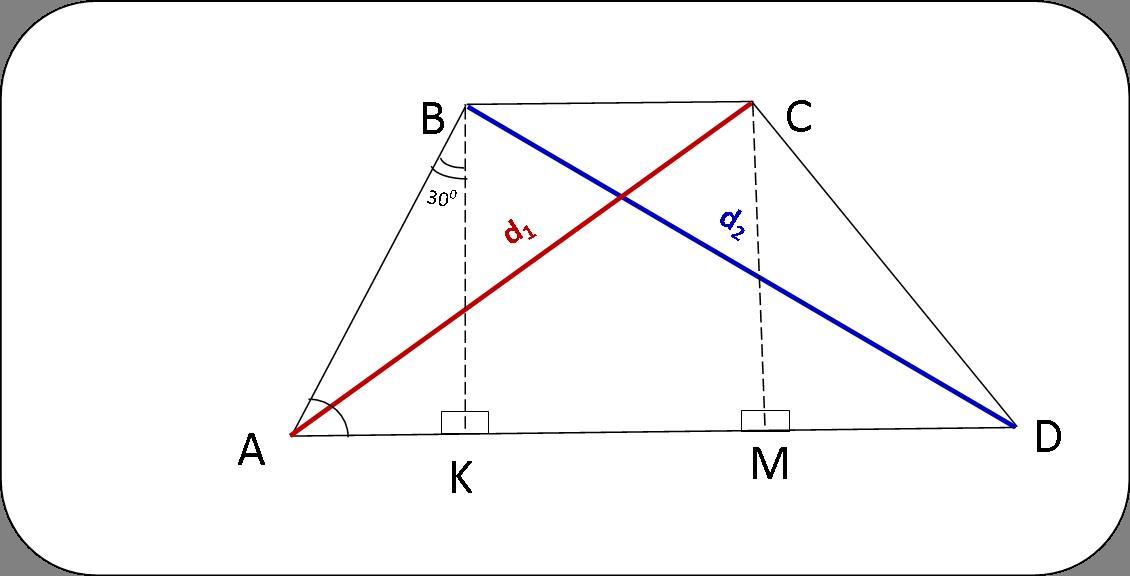
основи трапеції дорівнюють 6 і 16. одна з бічних сторін дорівнбє 10 см і утворює з більшою основою кут 60. знайдіть діагоналі трапеції
Ответы
1) Опустим перпендикуляры из вершин В и С.
ВК⊥AD и CM⊥AD
2) Рассмотрим ΔАВК.
∠ВАК = 60° по условию;
∠АКВ = 90° по построению;
∠АВК = 180° - (90°+60°) = 30°
2) Катет АК против угла 30°, потому он равен половине гипотенузы АВ.
АК = 10 см : 2 = 5см
3) По построению ВК⊥AD и CM⊥AD, значит,
KBCM - прямоугольник ==> BC = KM = 6 см
ВК = СМ
4) АМ = АК + КМ
АМ = 5см + 6см = 11см
5) МD = АD - АК
МD = 16см - 11см = 5см
6) Если AK = MD = 5см,
∠AKB = ∠BMD = 90°
ВК = СМ
значит, ΔАВК = ΔCDM => AB = CD => ABCD - равнобочная трапеция => значит её диагонали равны между собой.
7) ΔАВК -прямоугольный, значит, можно применить теорему Пифагора.
АК² + ВК² = АВ²
ВК² = 10² - 5²
ВК =
ВК = СМ =
7) ΔАСМ -прямоугольный. По теореме Пифагора найдем АС.
АС² = АМ² + СМ²
АС² = 11² + ()²
АС = см
АС = 14 см
8) AC = BD = 14см
Ответ: 14см; 14см