Предмет: Алгебра,
автор: sashakristosov30
2) В двух сосудах содержится два раствора уксусной кислоты. B первом сосуде — 30%-ный раствор, во втором сосуде — 6%-ный раствор. Сколько грамм каждого раствора нужно взять, чтобы Получить 1 л 24%-ного раствора?
Даю 15 баллов
Ответы
Автор ответа:
0
Объяснение:
значения взяты из таблицы
Приложения:
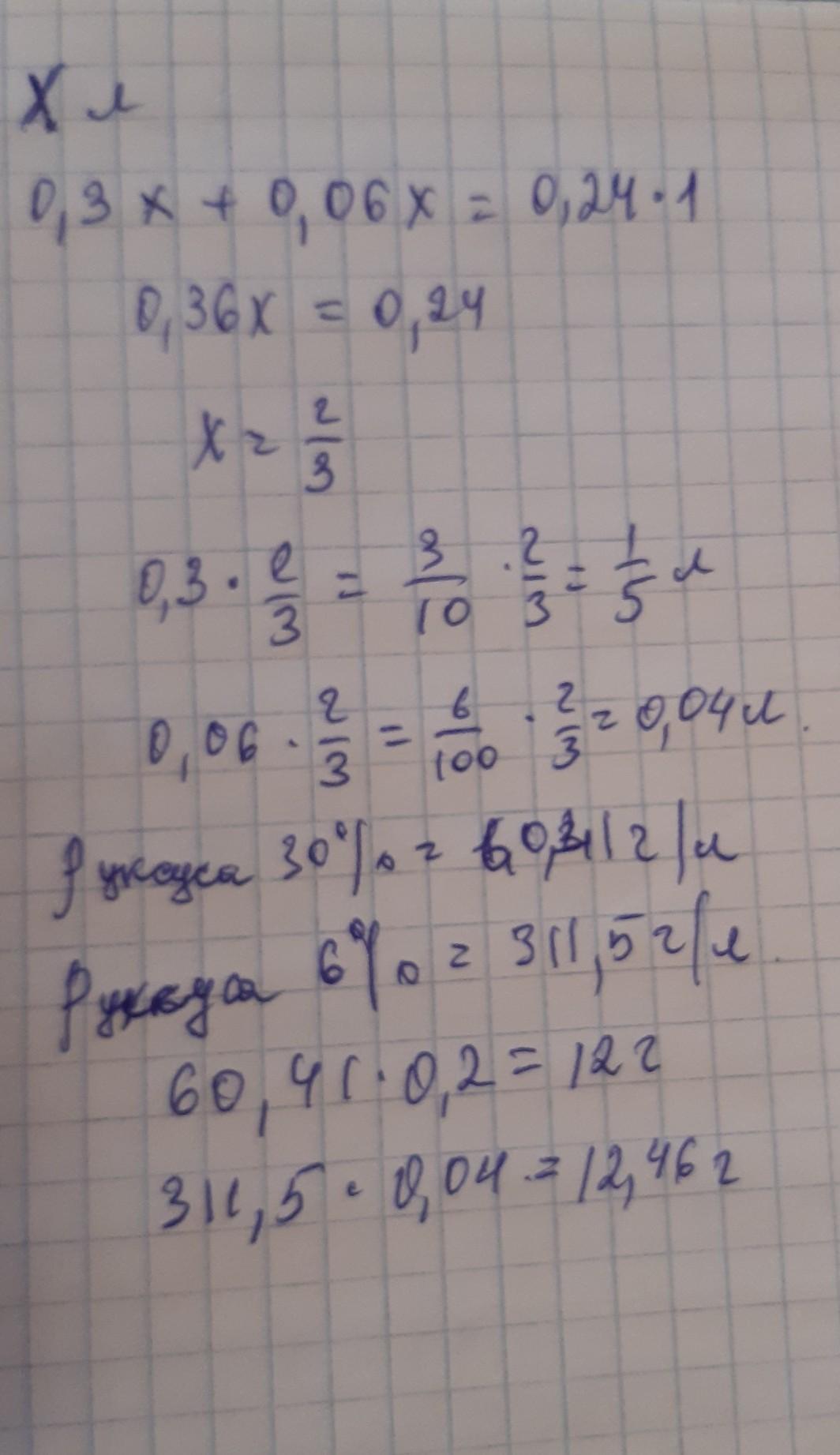
NNNLLL54:
0,06х ??? растворов же не одинаковое количество
х -литров так и обозначила ,
растворов разное количество по условию, поэтому один раствор - "х" , а другой - "у" --> 0,06y ...
ок
Автор ответа:
0
Ответ:
0.75 литров первого раствора +
0.25 литров второго раствора
Объяснение:
В 1 литре (=1000 мл) первого раствора 30% уксуса, то есть 1000*0.3=300 мл уксуса.
В литре второго раствора 6%, то есть 1000*0.06=60 мл уксуса.
Если возьмем x литров первого раствора, то уксуса будет взято x*30% = x*0.3 литров. Если возьмем y литров первого раствора, то уксуса будет взято y*6%=y*0.06 литров. По условиям x*0.3 +y*0.06 должен содержать 24% уксуса, то есть x*0.3 +y*0.06=0.24. При этом еще знаем, что должен получиться литр раствора, то есть x+y=1
x=1-y - подставляем в первое уравнение:
0.3x +0.06y=0.24
0.3*(1-y) +0.06y=0.24
0.3 -0.3y+0.06y=0.24
0.3 -0.24y=0.24
0.24y=0.3 -0.24
0.24y=0.06
y=0.06/0.24=0.25
x=1-0.25=0.75
описка: "у" литров 2-го, а не первого, раствора надо написать
да, опечатка. но исправить не могу :) Если возьмем y литров второго раствора
Похожие вопросы
Предмет: Українська мова,
автор: darinahappy
Предмет: Русский язык,
автор: аленаз2
Предмет: Английский язык,
автор: Iraira5
Предмет: Математика,
автор: Tomi200