Помогитеее пжж
Расставьте в вершинах кубика числа от 1 до 8 так, чтобы сумма четырёх чи-сел в вершинах одной грани была одной и той же для всех шести граней.
Ответы
Відповідь:
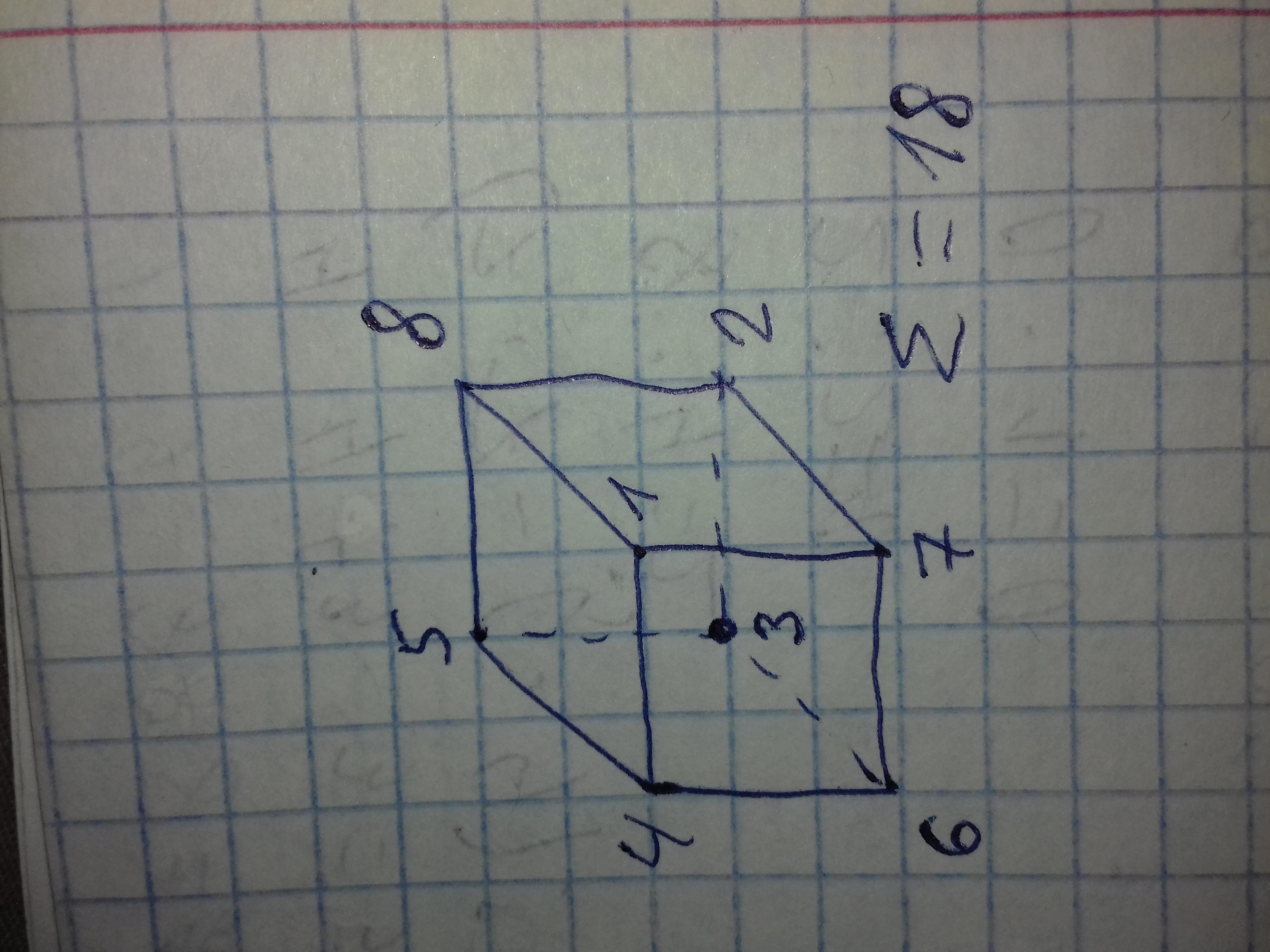
Решение на рисунке.
Покрокове пояснення:
Сумма ряда 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36. На каждой грани в ее вершинах находится четыре числа, то есть половина ряда, значит сумма чисел на каждой грани равна 36 / 2 = 18.
Пусть на верхней грани стоит число 8, значит в сумма чисел в остальных трех углах верхней грани равно 18 - 8 = 10. Пусть эти числа будут 5 + 4 + 1 = 10.
На боковой грани - два числа 8 и 1, значит сумма чисел внизу боковой грани равна 18 - 8 - 1 = 9. Из оставшихся чисел 2, 3, 6 и 7 можно создать две пары с суммой 9, это 2 + 7 = 9 и 3 + 6 = 9. Берем числа 7 и 2.
Передняя грань - есть числа 4, 1 и 7 недостает числа 18 - 4 - 1 - 7 = 6.
Вторая боковая грань - есть числа 5, 4 и 6 нехватает числа 18 - 5 - 4 - 6 = 3.
Проверяем заднюю грань 5 + 8 + 2 + 3 = 18.
Проверяем нижнюю грань 3 + 2 + 7 + 6 = 18.
Сумма на всех шести граням равна 18.