Предмет: Алгебра,
автор: cyutuber
Упростите выражения:
Приложения:
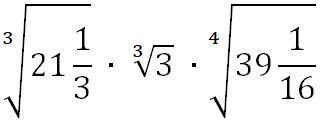
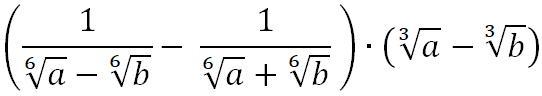
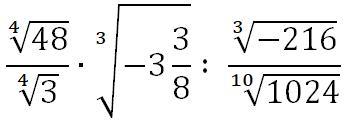
Ответы
Автор ответа:
3
cyutuber:
спасибо!
Пожалуйста
Автор ответа:
1
Ответ:
10
1
Объяснение:
1)
2)
3)
Похожие вопросы
Предмет: Английский язык,
автор: galka7575
Предмет: Русский язык,
автор: rincho13
Предмет: Қазақ тiлi,
автор: Amir112
Предмет: Русский язык,
автор: mouseadilya
Предмет: Литература,
автор: 19862827