Срочно решите пожалуйста,даю 25 баллов!!!!!!!!!!!!!!!
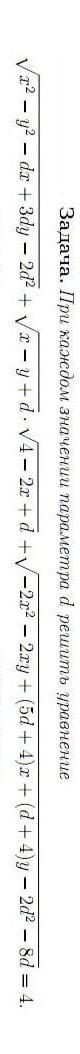
Ответы
Непростая задача и неудачные обозначения. Обозначать параметр буквой d может только человек, не уважающий дифференциал (шутка, но не совсем). Из-за этого, а также по причине того, что в дальнейшем фигурируют половинки d, предлагаю сразу обозначить d/2, скажем, буквой p. Преобразуем подкоренные выражения:
Последний корень не поместился на этой строчке; надеюсь каждый сумеет сам его выписать. Замена x-p=a; y-3p=b; после элементарных упрощений получаем
Для каждого из слагаемых в левой части применим неравенство Коши между средним арифметическим и средним геометрическим неотрицательных чисел причем равенство бывает только при u=v. Получаем, что левая часть не больше, чем
а нам нужно, чтобы левая часть равнялась четырем. Вывод:
a-b=a+b=-2a+4; то есть b=0, a=4/3, откуда x=4/3+d/2; y=3d/2.
Ответ: