Предмет: Математика,
автор: Аноним
хотелось бы объяснение каждого шага, а то я не понимаю решение...
Приложения:
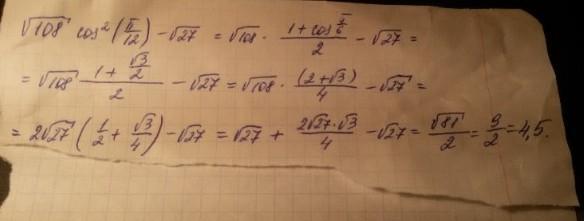
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
здесь применяются формулы
- это тригонометрия
и потом применяется выведение из-под корня и введение под корень
вот как делалось.
сначала применили тригонометрическую формулу
потом подставили значение косинуса и посчитали получившуюся дробь
и вот теперь выносим из-под корня
дальше просто расписали дробь
и получили
здесь √27 и -√27 сократились и дальше считаем только оставшуюся дробь
вот и всё.....
pushpull:
в числителе сложили 1+ √3/2 = (2 +√3)/2 и потом это поделили на знаменатель 2 и получится (2+√3)/4
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: violetta106
Предмет: Русский язык,
автор: niv22
Предмет: Алгебра,
автор: nanogel
Предмет: Литература,
автор: dashakolodko503