Question

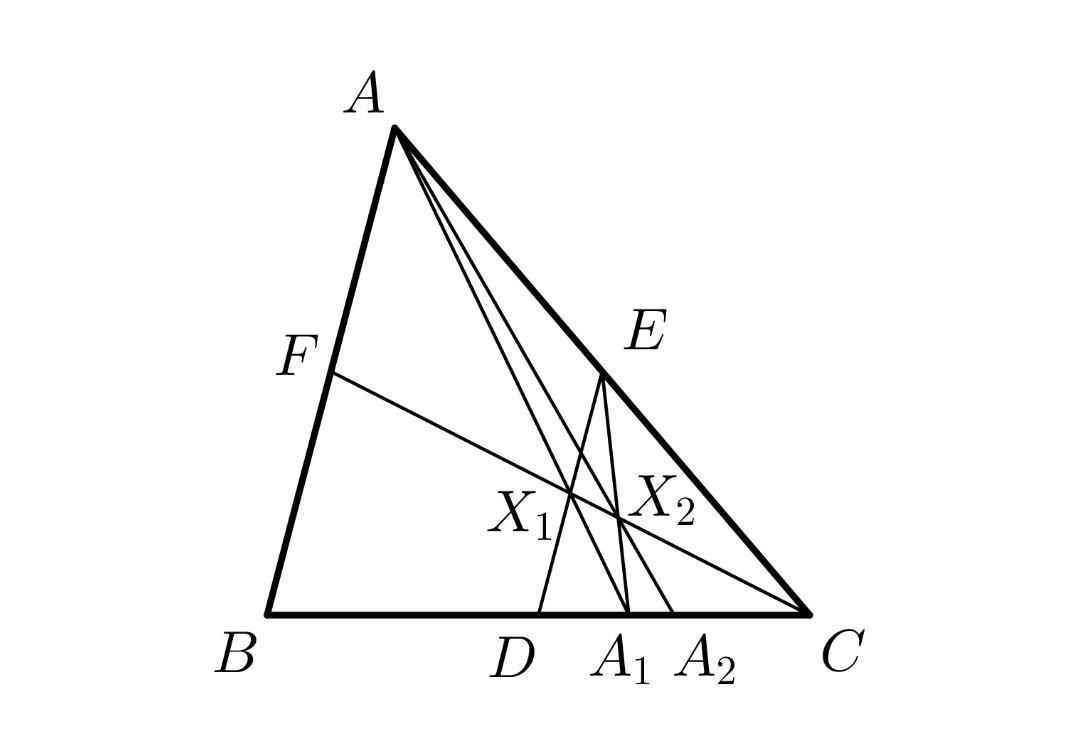
Точки D, E, F — середины сторон BC, AC, AB треугольника ABC соответственно. X1 — точка пересечения прямых DE и CF, A1 — точка пересечения прямых AX1 и BC. X2 — точка пересечения прямых A1E и CF, A2 — точка пересечения прямых AX2 и BC. Аналогично определяются точки X3, A3, X4, A4, …, X10, A10. Найдите отношение CA10:A10B.

Answer 1

Я решил поместить тут решение с использованием проективных пучков из личных практических целей, - мне это нужно для возможности потом ссылаться. Если кого-то не устраивает - можно пожаловаться, и удалить, я не буду переживать.

Пусть M - точка пересечения медиан (в частности, AD и BE). Два проективных пучка с центрами A и E определяют соответствие последовательностей точек F, M, X1, X2, .... C <=> B, D, A1, A2,... C (центр A) и M, X1, X2 .... C <=> B, D, A1, A2 .... C (центр E).

Двойные отношения (A,B,C,D)=(AC/CB):(AD/DB) для 4 любых коллинеарных точек A B C D при проективном преобразовании остаются неизменными, поэтому (F,M, X1,C)=(B,D,A1,C)=(M,X1,X2,C)=(D,A1,A2,C) =.....=(A8,A9,A10,C) = ....

На каждой из секущих FC и BC можно принимать свою меру длины, удобнее всего считать FC = 1 на прямой FC и BC = 1 на прямой BC. Величины двойных отношений не зависят от этого, главное - не перепутать прямые :)

Величина двойного отношения легко считается - пусть FC = 1, тогда FX1 = 1/2 = СX1 (по модулю), FM = 1/3, CM = 2/3; X1M = 1/6;

(F,M,X1,C)= (1/2)/(1/6):(1/(2/3)) =2;

Легко найти что A1D = 1/6; (этот же результат мгновенно дает теорема Ван-Обеля, которую можно применить для получения точки A1: 2CA1/BA1 = CX1/FX1, 2(1/2-z)/(1/2+z) = 1; z = A1D = 1/6)

Дальше можно сосчитать всю последовательность A2, A3 и так далее. Чтобы сэкономить, я предполагаю вот что (на самом деле уже зная ответ :) ). Для того, чтобы немного формализовать и сделать более удобной работу с последовательностью, я приму другие обозначения  

Пусть P(0)=B, P(1)=D; P(2)=A(1) ..... Я предполагаю, что длина отрезка P(k-1)P(k)=1/k(k+1)=1/k-1/(k+1); это соответствует первым 4-5 точкам, которые легко считаются, включая и отрезок BD = P(0)P(1) = 1/(1*2) = 1/1 - 1/2;

Нужно показать, что (P(k-1),P(k),P(k+1),1)=2;

BP(k) = 1/(1*2) + 1/(2*3) + .... + 1/k(k+1) = (1 - 1/2) +(1/2 - 1/3) + .... + (1/k - 1/(k+1)) = 1 - 1/(k+1); CP(k) = 1/(k+1);

P(k-1)P(k+1)/(P(k+1)P(k)):(P(k-1)C/CP(k)) = (1/(k(k+1)) + 1/((k+1)(k+2))/(1/(k+1)(k+2)):((1/k)/(1/(k+1)))) = (2k+2)/k : (k/(k+1))  = 2;

Таким образом, выбранная последовательность удовлетворяет двойному отношению. То есть по точкам P(k-1), P(k) и C однозначно определяется точка P(k+1) - в противном случае возникало бы противоречие с тем, что существует только одна точка на отрезке, делящая его в заданном отношении (простом разумеется). И так для любого k. Метод математической индукции позволяет заключить, что все точки P(k) на прямой BC удовлетворяют этой последовательности.

Осталось найти CA10/BA10. Точка A10 соответствует P(11), то есть

CA10 = 1/12; BA10 = 11/12; CA10/BA10 = 1/11;

тут вообще интересная последовательность CD/BD = 1; CA1/BA1 = 1/2; CA2/BA2 = 1/3 и так далее.