Предмет: Геометрия,
автор: abc620
На рёбрах CD и BB1 куба ABCDA1B1C1D1 с ребром 12 отмечены точки Р и Q соответственно, причём DP = 4, а B1Q = 3.
Найдите расстояние от точки С до плоскости APQ.
Ответы
Автор ответа:
4
Пусть С - начало координат.
Ось X - CD
Ось Y - CB
Ось Z - CC1
координаты точек
A(12;12;0)
P(8;0;0)
Q(0;12;9)
Уравнение плоскости APQ
ax+by+cz+d =0
подставляем координаты точек A P Q
12a+12b+d=0
8a+d=0
12b+9c+d=0
Пусть d= -24 , тогда a=3 b= -1 c = 4
Уравнение плоскости
3x - y +4z -24 =0
Нормальное уравнение плоскости
k= √(3^2+1^2+4^2) = √26
3x/k-y/k+4z/k-24/k=0
Подставляем координаты точки C (0;0;0)
в нормальное уравнение плоскости
Искомое расстояние
24/√26
abc620:
это метод координат? Блин - мы еще не изучали. Я только в 11 перехжу...
Ну что ж я то могу поделать? )) Учи - другого пути нет ... Обычным способом - это час на ЕГЭ потерять )))
Автор ответа:
4
Ответ:
Другой путь ( без y , z , x и прочей х ... )
Объяснение:
Приложения:
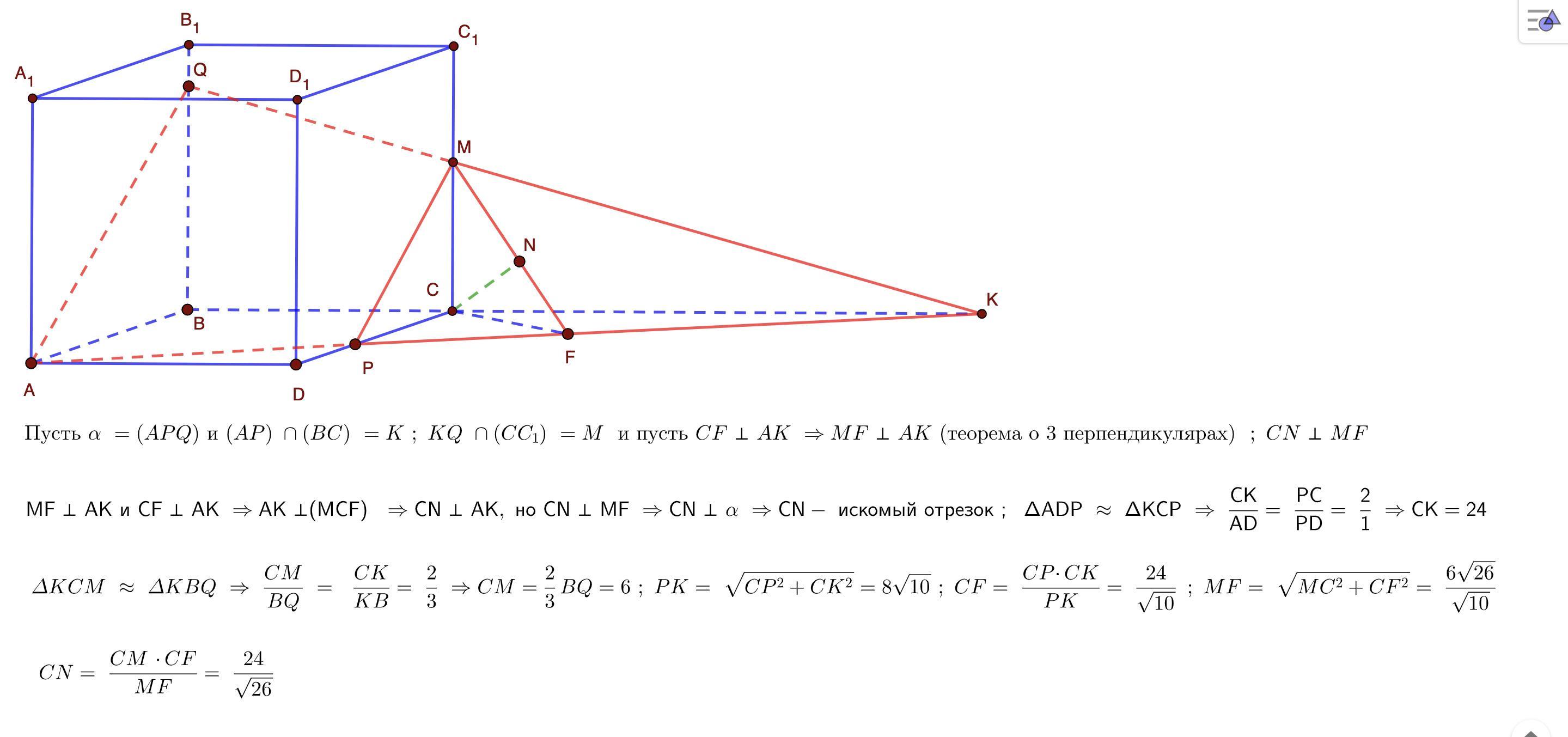
В решении использовано утверждение : высота прямоугольного треугольника , проведённая к гипотенузе равна отношению произведения катетов к гипотенузе ( 2 S = ab = ch = > h = (ab) / c )
спасибо
Похожие вопросы
Предмет: Русский язык,
автор: bazanova834
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Ракана
Предмет: Алгебра,
автор: smirnova55555w
Предмет: Математика,
автор: Андрюшка332