Предмет: Алгебра,
автор: Аноним
Нужно решить задачу, помогите
Приложения:
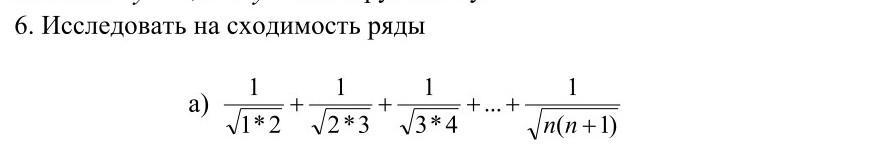
antonovm:
используя предельный признак сравнения сравните этот ряд с гармоническим , предел равен 1 , гармонический расходится , значит и этот расходится
Ответы
Автор ответа:
1
Ответ:
Сравним с рядом расходящийся
гармонический ряд .
Расходится мажорантный ряд ⇒ нельзя сделать вывод о сходимости миноранты . Применим предельный признак сравнения.
оба ряда ведут себя одинаково, то есть расходятся .
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: супергерлбедмун
Предмет: Русский язык,
автор: Firestare
Предмет: Алгебра,
автор: р1р2р3р4р5р6
Предмет: Литература,
автор: мухамед38