Предмет: Математика,
автор: iliyberdnikov
РЕБЯТА ПОМОГИТЕ СРОЧНО
БАЛЛАМИ НЕ ОБИЖУ
Приложения:
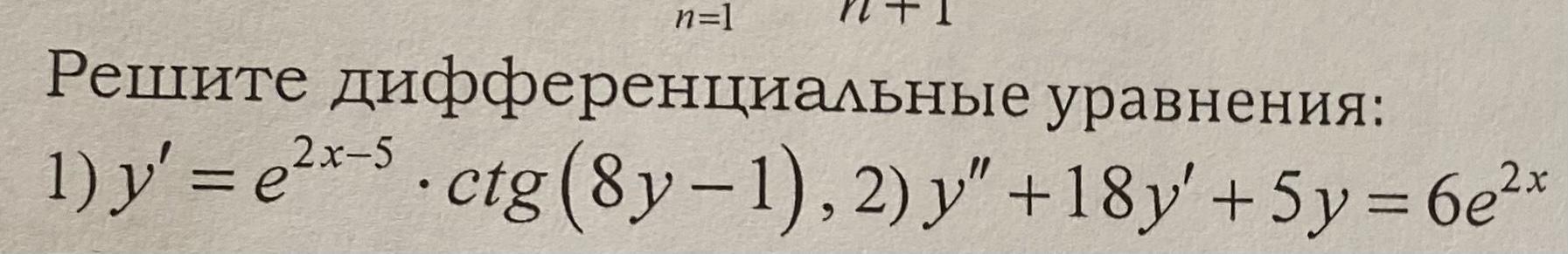
tatsach:
Больше того, что вы в баллах написали, добавить не получится
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: МаринаK2015
Предмет: Русский язык,
автор: Мейсарат280603
Предмет: Английский язык,
автор: sahuly1222
Предмет: Русский язык,
автор: altkseykal2012
Предмет: ОБЖ,
автор: ElenaKarakatitca