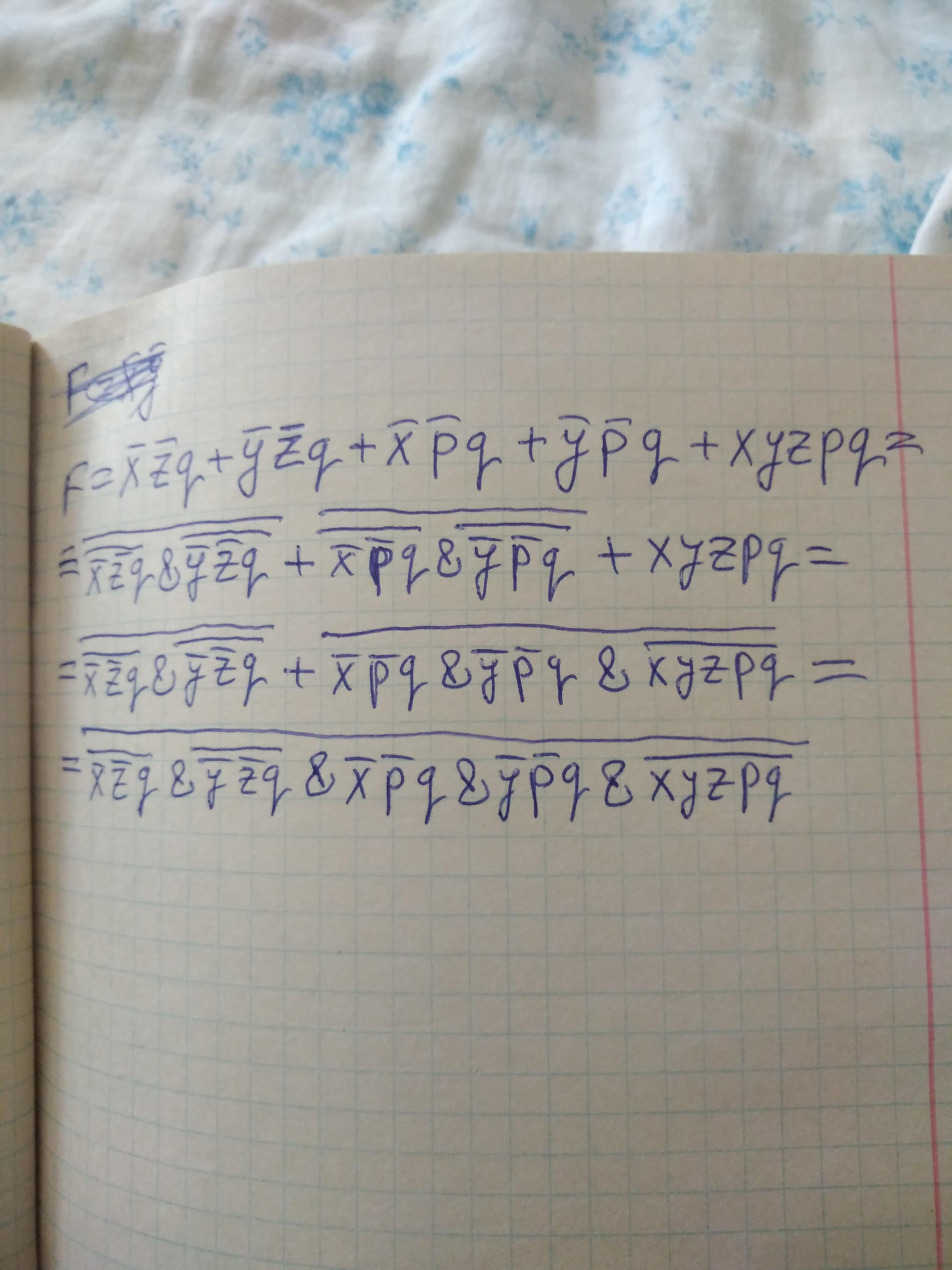помогите с заданием:
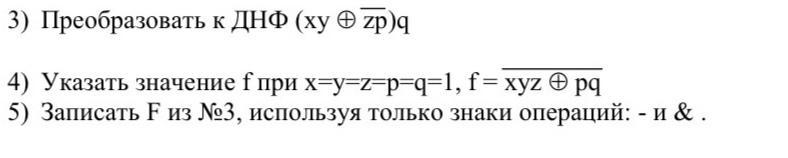
Ответы
Ответ:
Объяснение:
Сразу напишу, что знак ⊕ означает сложение по модулю 2 и имеет такую таблицу истинности:
a | 0 | 0 | 1 | 1
b | 0 | 1 | 0 | 1
⊕| 0 | 1 | 1 | 0
Иначе говоря, если a = b, то a⊕b = 0, а если a ≠ b, то a⊕b = 1.
Ее можно преобразовать так:
a⊕b = (~a)&b + a&(~b)
Здесь и далее ~a означает отрицание а.
3) ДНФ - дизъюнктивная нормальная форма,
F = (xy ⊕ ~(zp) )q = (~(xy)&~(zp) + xy&zp) & q = ((~x+~y)&(~z+~p) + xyzp) & q =
= ( (~x)(~z) + (~y)(~z) + (~x)(~p) + (~y)(~p) + xyzp) & q =
= (~x)(~z)q + (~y)(~z)q + (~x)(~p)q + (~y)(~p)q + xyzpq
4) f = ~(xyz⊕pq) = ~( ~(xyz)&pq + xyz&~(pq)) )
Если x = y = z = p = q = 1, то
f = ~( ~(1&1&1)&(1&1) + (1&1&1)&~(1&1)) ) = ~( ~(1)&1 + 1&~(1) ) = ~( 0&1) = ~0 = 1
5) Функция F из №3, используя только ~ и &
F = (~x)(~z)q + (~y)(~z)q + (~x)(~p)q + (~y)(~p)q + xyzpq
Решение смотрите на фото.
Все операции умножения можно заменить на &. Например:
~x~zq = ~x & ~z & q