ПОМОГИТЕ, ПОЖАЛУЙСТА! Дам 20 баллов!
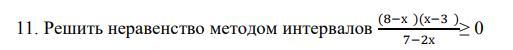
Ответы
Ответ:
x∈[3;3,5)U[8;+∞)
Пошаговое объяснение:
Чтобы решать через метод интервалов нужно сначала найти нули выражения.
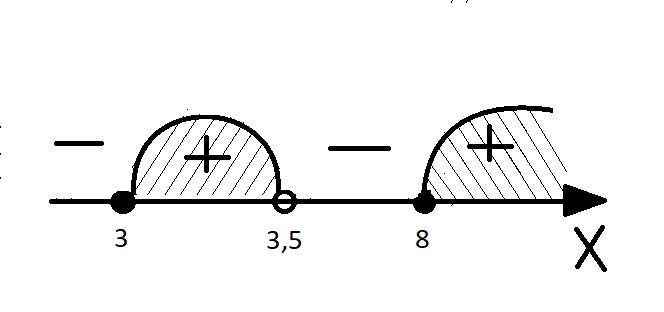
Теперь расставим эти значения на координатной прямой(см. вложение)
Т.к. Знак неравенства нестрогий, то мы закрашиваем все точки кроме x=3,5, потому что 7-2x стоит в знаменателе.
Теперь определяем знак самого левого промежутка, после их знаки чередуются. Для поверки можно на каждом промежутке взять какое-нибудь число и подставить его в выражение.
При x=0:
Знак отрицательный, значит ставим "-"
При x=3,1:
Знак положительный, значит ставим "+"
При x=4:
Знак отрицательный, значит ставим "-"
При x=9:
Знак положительный, значит ставим "+"
Теперь, когда мы расставили все знаки, то выбираем нужные промежутки(там,где стоит "+")
Смотрим на рисунок и пишем ответ, что x∈[3;3,5)U[8;+∞)