Предмет: Другие предметы,
автор: vladrobocop551
Помогите, пожалуйста, с высшей математикой. Тема
Интегральное исчисление функции одной переменной
Приложения:
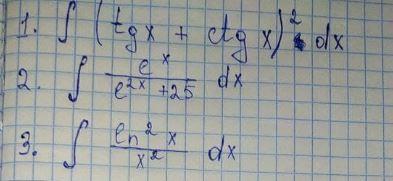
Ответы
Автор ответа:
0
Ответ:
1. -2ctg2x + C
2. 0,2arctg(0,2e^x) + C
3. -ln²x / x - 2ln x / x - 2/x + C
Объяснение:
1.
2.
3.
Похожие вопросы
Предмет: Русский язык,
автор: 2494702
Предмет: Русский язык,
автор: kris252
Предмет: Русский язык,
автор: olesyapavlova1
Предмет: Математика,
автор: Sonyapeppercan