Предмет: Математика,
автор: matveiblack
Решите неравенство. Пожалуйста с объяснением. Математика 9-10 класс.
Приложения:
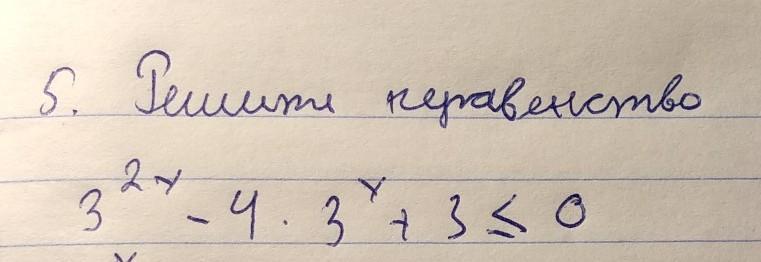
Ответы
Автор ответа:
2
Решение неравенства прикреплено.
k ∈ [1 ; 3]
∈ [1 ; 3]
x ∈ [0 ; 1]
Ответ: x ∈ [0 ; 1]
Приложения:
Автор ответа:
2
Ответ:
Пошаговое объяснение:
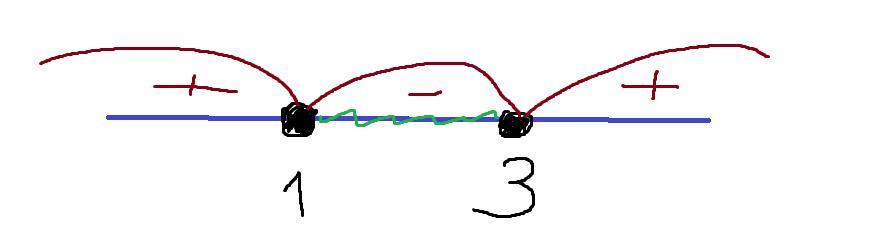
По методу интервалов имеем, что это неравенство выполняется, если
Аноним:
ʏᴇ?
Похожие вопросы
Предмет: Русский язык,
автор: Smirveronichka
Предмет: Английский язык,
автор: gorboelena1
Предмет: Русский язык,
автор: PokatilovaVicka
Предмет: Українська мова,
автор: professionaltype