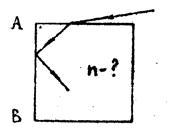
Для любого луча, падающего на верхнюю грань прозрачного куба, наблюдается пол-ное отражение на боковой грани AB (рис.6). При каком минимальном показателе преломления материала куба это возможно?
Ответы
Возьмём теорию предельного угла отражения. В качестве падающего обычно рассматривается луч, идущий из оптически более плотной среды (из куба). При угле преломления, равном 90°, падающий луч называют предельным углом отражения α₀:
sinα/sinβ = n₂/n₁ = 1/n
где α - падающий луч (идущий из куба)
β - преломлённый луч
n₁ - абсолютный показатель преломления материала куба
n₂ - абсолютный показатель преломления воздуха, примерно равный единице (n₂ = 1)
n - относительный показатель преломления двух сред (в нашей задаче это и есть искомый показатель преломления материала куба: n₁ = n)
β = 90° => α = α₀ =>
=> sinα₀ = 1/n
Выразим из уравнения n:
sinα₀ = 1/n
n = 1/sinα₀
В задаче просят найти минимальное значение показателя. Очевидно, что оно будет таковым только в том случае, если sinα₀ будет максимальным. А синус угла α₀ тем больше, чем больше сам угол α₀, следовательно:
n_min = 1/sinα₀_max
Будем рассуждать исходя из изображённого на рисунке направления луча: угол преломления луча в кубе назовём предельным углом отражения, если угол падающего луча на верхнюю грань будет равен 90°.
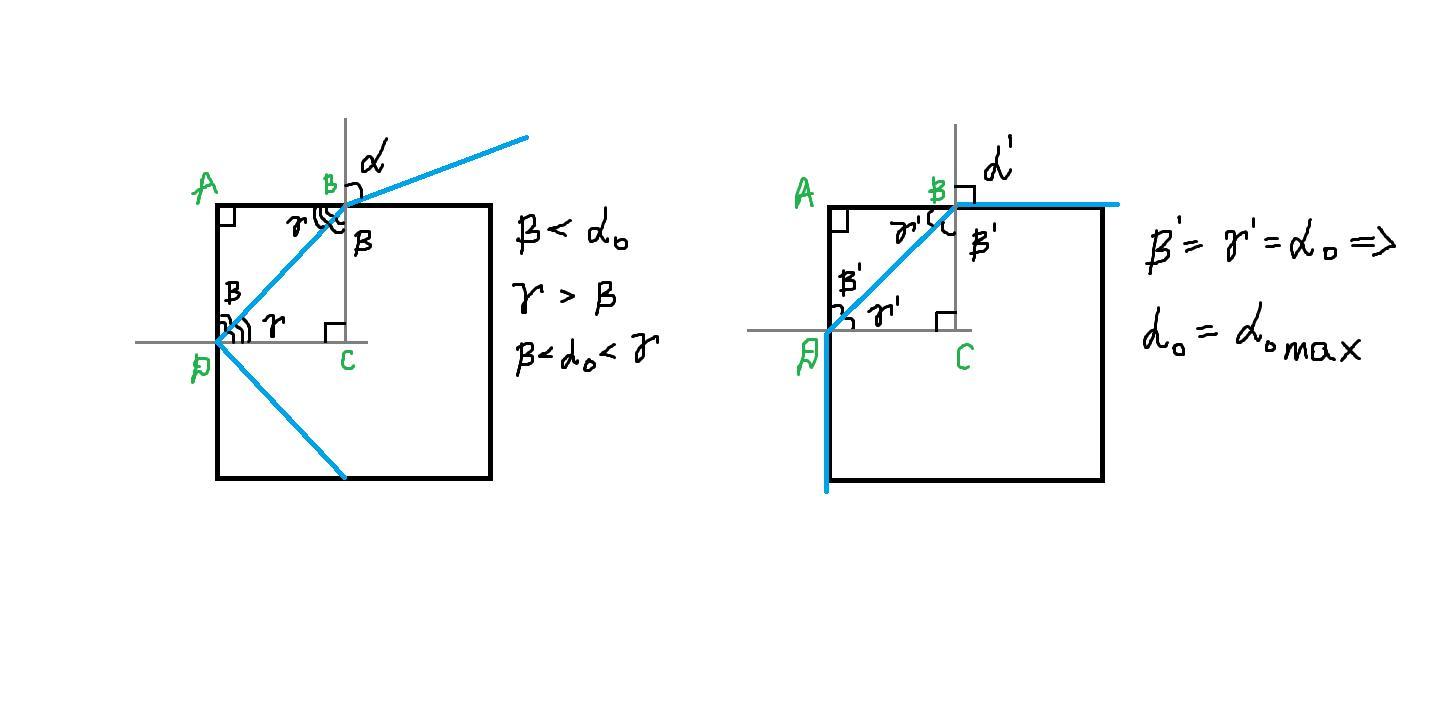
Обратимся к рисунку. Выясним углы преломления и отражения - меньше они или больше, чем α₀.
Если преломлённый луч β полностью отражается от боковой грани, то угол отражения γ должен быть больше предельного угла α₀. Значит:
γ > α₀
Падающий луч преломляется, его направление даже близко нельзя назвать параллельным грани, значит угол преломления β меньше, чем предельный угол отражения α₀:
β < α₀
Следовательно, мы можем указать такое взаимоотношение углов:
β < α₀ < γ
Рассмотрим четырёхугольник ABCD (см. рисунок). Углы СDB(γ) и ABD, СBD(β) и ADB равны, т.к. являются накрест лежащими. Сумма углов любого четырёхугольника равна 360°. Наш четырёхугольник является прямоугольником (но не квадратом), т.к. все его углы прямые. Два угла очевидны (углы А и С равны 90°), а каждый из оставшихся двух равен сумме: β + γ = 90°.
Теперь попробуем мысленно рассмотреть другие лучи, угол падения которых больше или меньше, чем представленный на рисунке. Если угол падения луча будет меньше, то угол преломления тоже станет меньше, а угол отражения - больше. Если же угол падения будет больше, то всё окажется наоборот: угол преломления станет больше, а угол отражения - меньше.
Мы уже выяснили, что на рисунке углы β и γ представлены в сравнении:
β < α₀ < γ
α₀ - это константа. Этот угол зависит только от абсолютных показателей преломления граничащих сред. Сумма (β + γ = 90°) - тоже константа. Как бы мы ни изменяли значения β и γ, их сумма будет оставаться постоянной. Другими словами, опираясь на рисунок: какой бы мы прямоугольник ABCD ни рассматривали, сумма углов (β + γ = 90°) всегда будет сохраняться. Следовательно, если
α₀ = сonst. и β + γ = сonst., то
β + γ + α₀ = сonst.
ИЛИ
β' + γ' + α₀ = сonst., где β' = α₀
Значит, если угол β' будет равен углу α₀, то угол γ' окажется либо меньше, либо больше, чем угол α₀, либо же равен ему. Получаем несколько условий:
γ' < α₀ при β' = α₀
γ' > α₀ при β' = α₀
γ' = α₀ при β' = α₀
Первое неравенство бессмысленно, поскольку согласно данным задачи любой падающий на верхнюю грань луч должен полностью отражаться от грани АВ - а это возможно только в том случае, если γ' > α₀.
Нам нужно, чтобы β' было максимальным и при этом выполнялось условие полного отражения. Если γ' > α₀, то γ' > β'. В этом случае условия задачи выполняются частично - луч испытывает полное отражение, но β' не является максимальным, ведь:
β' + γ' = 90°, γ' > β', тогда если γ' = 46°, то β' = 90° - γ' = 90° - 46° = 44°,
a 44° < 45°
Остаётся только уравнение:
γ' = α₀ при β' = α₀
γ' = β' => β' + β' = 2β' = 90° => β' = 90°/2 = 45°
α₀_max = 45°
Действительно, при угле в 45° выполняются оба условия, и они не противоречат друг другу:
1) показатель преломления минимален
2) для любого падающего луча наблюдается полное отражение на грани АВ
Для любого, кроме падающего параллельно. Ведь в реальности луч не может падать на грань параллельно и преломляться, или идти, например, из стекла и выходить параллельно его поверхности. Это всего лишь допущение, призванное обозначить границу возможного.
Остаётся найти значение n:
n_min = 1/sinα₀_max = 1/sin45° = 1/(√2/2) = 1*2/√2 = 2/√2 = √2 ≈ 1,41
Ответ: приблизительно 1,41.