Question

Найдите площадь фигуры, ограниченной графиком функции.

Answer 1

Ответ:

Пошаговое объяснение:

$\displaystyle S=\int\limits^2_{-1} {(-x^2+x+2) } \, dx =\bigg (-\frac{x^3}{3} +\frac{x^2}{2} +2x \bigg )\bigg |_{-1}^2=3+\frac{3}{2} +6=\frac{21}{2}$

Answer 2

Ответ:

4.5

Пошаговое объяснение:

$y=-x^2+x+2=-(x^2-x-2)=-(x^2-2*0.5x+0.5^2-2.25)=\\-((x-0.5)^2-2.25)=-(x-0.5)^2+2.25$

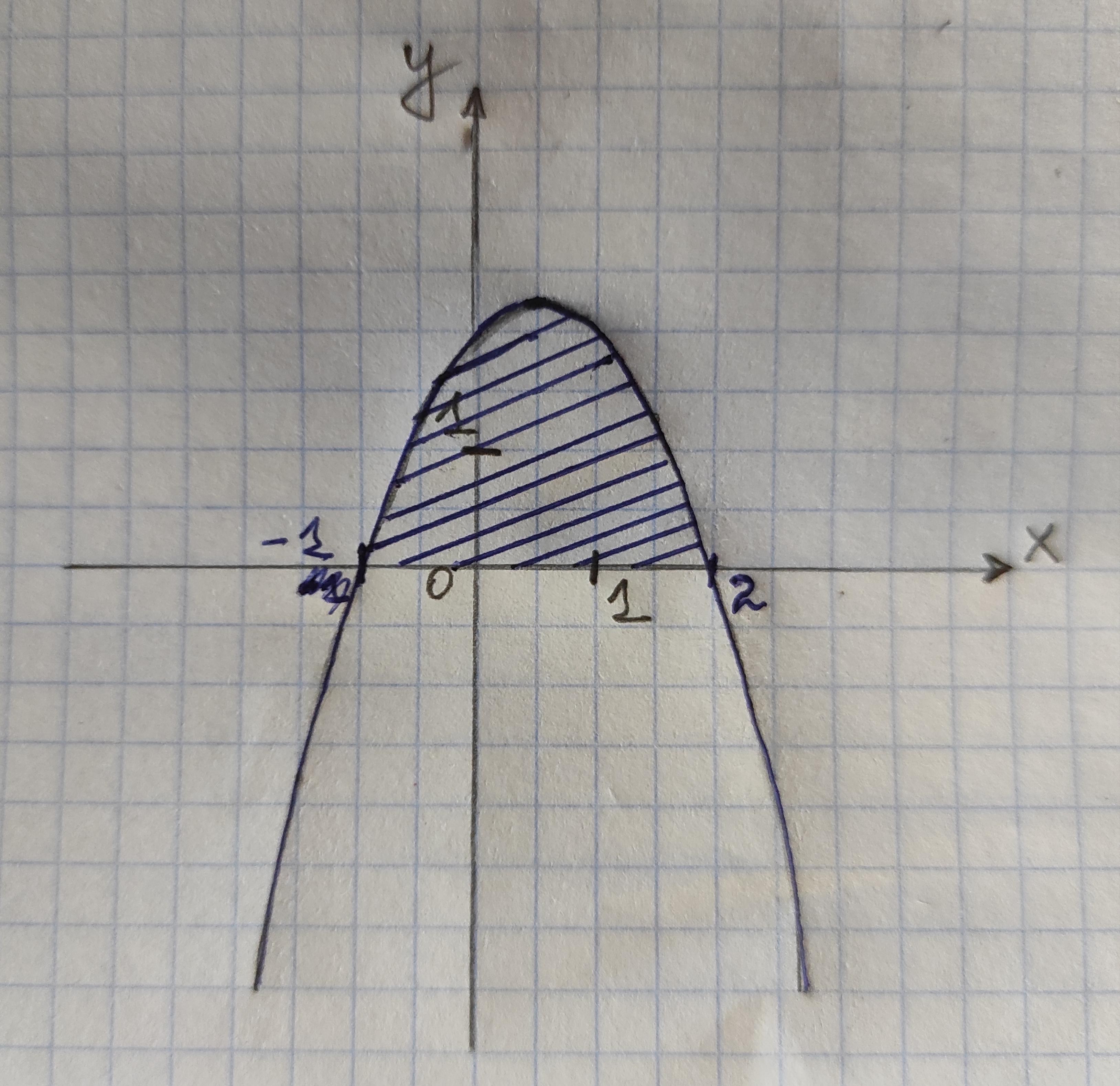
График функции — это парабола y=x², перенесенная сначала на 0,5 единицы вправо, затем симметрично отраженная относительно оси абсцисс и в конце перенесенная на 2,25 единицы вверх (смотри вложение).

Найдем пределы интегрирования — нули заданной функции:

$-x^2+x+2=0\\x^2-x-2=0$

По теореме Виета

$\begin{cases} x_1+x_2=1\\x_1*x_2=-2 \end{cases}\\\begin{cases} x_1=-1\\x_2=2 \end{cases}$

Получили, что площадь заштрихованной фигуры (криволинейной трапеции) равна определенному интегралу от y на отрезке [-1; 2].

$S=\int\limits^2_{-1} {(-x^2+x+2)} \, dx =-\frac{x^3}{3}+\frac{x^2}{2}+2x \bigg|_{-1}^2=-\frac{2^3}{3}+\frac{2^2}{2}+2*2-\\(-\frac{(-1)^3}{3}+\frac{(-1)^2}{2}+2*(-1))= -\frac{8}{3}+2+4-\frac{1}{3}-\frac{1}{2}+2=4.5$