Предмет: Алгебра,
автор: kotorisanru
Найти производные следущих функций
Подробно если можно
Ответы есть но мне нужно решение я что-то в этом профан
1)-tg2x✓cos2x
Приложения:
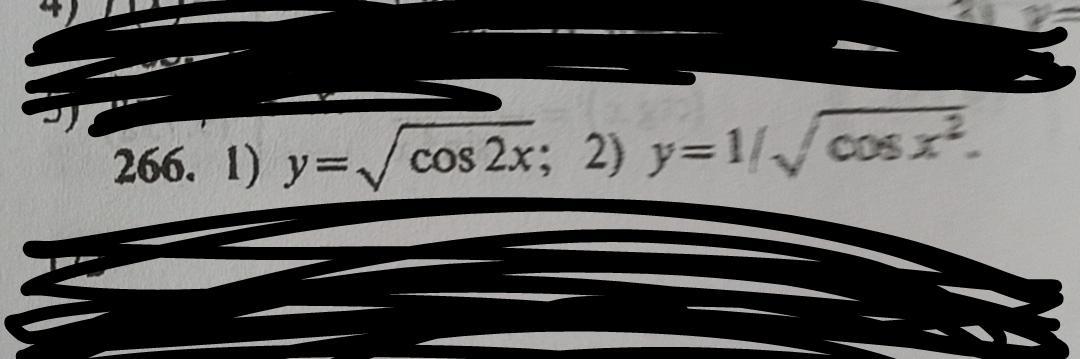
Ответы
Автор ответа:
1
Производную берем так же, как у обычных степенных функций: (х^а)' = а*х^(а-1),
НО функции сложные, нужно взять еще производные внутренних функций.
1.
2.
Похожие вопросы
Предмет: Русский язык,
автор: Романтина
Предмет: Окружающий мир,
автор: vvp2006
Предмет: Русский язык,
автор: asamso
Предмет: Українська мова,
автор: Аноним